Preliminaries

Package requirements

We start by loading a couple of packages for data manipulation, dimension reduction and fancy representations.

library(tidyverse)   # advanced data manipulation and vizualisation
library(knitr)       # R notebook export and formatting 
library(FactoMineR)  # Factor analysis
library(factoextra)  # Fancy plotting of FactoMineR outputs
library(corrplot)    # Fancy plotting of matrices 
library(GGally)      # Easy-to-use ggplot2 extensions
library(ggpubr)      # Easy-to-use ggplot2 exentesions
library(maps)        # Draw Geographical Maps
library(ggrepel)     # Automatically Position Non-Overlapping Text Labels with ggplot
theme_set(theme_bw()) # set default ggplot2 theme to black and white

Reminders on Multidimensional scaling (MDS)

There are different types of MDS algorithms, including

Classical multidimensional scaling Preserves the original distance metric, between points, as well as possible. That is the fitted distances on the MDS map and the original distances are in the same metric. Classic MDS belongs to the so-called metric multidimensional scaling category.

It is also known as principal coordinates analysis. It is suitable for quantitative data.

Non-metric multidimensional scaling It is also known as ordinal MDS. Here, it is not the metric of a distance value that is important or meaningful, but its value in relation to the distances between other pairs of objects.

Ordinal MDS constructs fitted distances that are in the same rank order as the original distance. For example, if the distance of apart objects \(1\) and \(5\) rank fifth in the original distance data, then they should also rank fifth in the MDS configuration.

It is suitable for qualitative data.

R functions for MDS

To perform MDS, we may either use:

cmdscale() [stats package]: Compute classical (metric) multidimensional scaling.

?cmdscale()

isoMDS() [MASS package]: Compute Kruskal’s non-metric multidimensional scaling (one form of non-metric MDS).

?isoMDS()

sammon() [MASS package]: Compute Sammon’s non-linear mapping (one form of non-metric MDS).

?sammon()

All of these functions take a distance object as main argument and a number \(k\) corresponding to the desired number of dimensions in the scaled output.

Classical MDS

We consider the swiss data that contains fertility and socio-economic data on 47 French speaking provinces in Switzerland.

Start by loading the swiss package and have a quick look at it.

data("swiss")
swiss %>% head(15)

##              Fertility Agriculture Examination Education Catholic
## Courtelary        80.2        17.0          15        12     9.96
## Delemont          83.1        45.1           6         9    84.84
## Franches-Mnt      92.5        39.7           5         5    93.40
## Moutier           85.8        36.5          12         7    33.77
## Neuveville        76.9        43.5          17        15     5.16
## Porrentruy        76.1        35.3           9         7    90.57
## Broye             83.8        70.2          16         7    92.85
## Glane             92.4        67.8          14         8    97.16
## Gruyere           82.4        53.3          12         7    97.67
## Sarine            82.9        45.2          16        13    91.38
## Veveyse           87.1        64.5          14         6    98.61
## Aigle             64.1        62.0          21        12     8.52
## Aubonne           66.9        67.5          14         7     2.27
## Avenches          68.9        60.7          19        12     4.43
## Cossonay          61.7        69.3          22         5     2.82
##              Infant.Mortality
## Courtelary               22.2
## Delemont                 22.2
## Franches-Mnt             20.2
## Moutier                  20.3
## Neuveville               20.6
## Porrentruy               26.6
## Broye                    23.6
## Glane                    24.9
## Gruyere                  21.0
## Sarine                   24.4
## Veveyse                  24.5
## Aigle                    16.5
## Aubonne                  19.1
## Avenches                 22.7
## Cossonay                 18.7

rownames(swiss)

##  [1] "Courtelary"   "Delemont"     "Franches-Mnt" "Moutier"      "Neuveville"  
##  [6] "Porrentruy"   "Broye"        "Glane"        "Gruyere"      "Sarine"      
## [11] "Veveyse"      "Aigle"        "Aubonne"      "Avenches"     "Cossonay"    
## [16] "Echallens"    "Grandson"     "Lausanne"     "La Vallee"    "Lavaux"      
## [21] "Morges"       "Moudon"       "Nyone"        "Orbe"         "Oron"        
## [26] "Payerne"      "Paysd'enhaut" "Rolle"        "Vevey"        "Yverdon"     
## [31] "Conthey"      "Entremont"    "Herens"       "Martigwy"     "Monthey"     
## [36] "St Maurice"   "Sierre"       "Sion"         "Boudry"       "La Chauxdfnd"
## [41] "Le Locle"     "Neuchatel"    "Val de Ruz"   "ValdeTravers" "V. De Geneve"
## [46] "Rive Droite"  "Rive Gauche"

summary(swiss)

##    Fertility      Agriculture     Examination      Education    
##  Min.   :35.00   Min.   : 1.20   Min.   : 3.00   Min.   : 1.00  
##  1st Qu.:64.70   1st Qu.:35.90   1st Qu.:12.00   1st Qu.: 6.00  
##  Median :70.40   Median :54.10   Median :16.00   Median : 8.00  
##  Mean   :70.14   Mean   :50.66   Mean   :16.49   Mean   :10.98  
##  3rd Qu.:78.45   3rd Qu.:67.65   3rd Qu.:22.00   3rd Qu.:12.00  
##  Max.   :92.50   Max.   :89.70   Max.   :37.00   Max.   :53.00  
##     Catholic       Infant.Mortality
##  Min.   :  2.150   Min.   :10.80   
##  1st Qu.:  5.195   1st Qu.:18.15   
##  Median : 15.140   Median :20.00   
##  Mean   : 41.144   Mean   :19.94   
##  3rd Qu.: 93.125   3rd Qu.:21.70   
##  Max.   :100.000   Max.   :26.60

Perform classical MDS with \(k=2\) and plot the results.

# Cmpute MDS
mds <- swiss %>%
  dist(method='euclidean') %>%          
  cmdscale() %>%
  as_tibble()

colnames(mds) <- c("Dim.1", "Dim.2")

mds %>% head(10)

## # A tibble: 10 x 2
##     Dim.1 Dim.2
##     <dbl> <dbl>
##  1  37.0  17.4 
##  2 -42.8  14.7 
##  3 -51.1  19.3 
##  4   7.72  5.46
##  5  35.0  -5.13
##  6 -44.2  25.9 
##  7 -56.4  -3.23
##  8 -61.3  -1.00
##  9 -56.4  12.3 
## 10 -47.5  19.9

# Plot MDS
ggscatter(mds, x = "Dim.1", y = "Dim.2", 
          label = rownames(swiss),
          size = 1,
          repel = TRUE)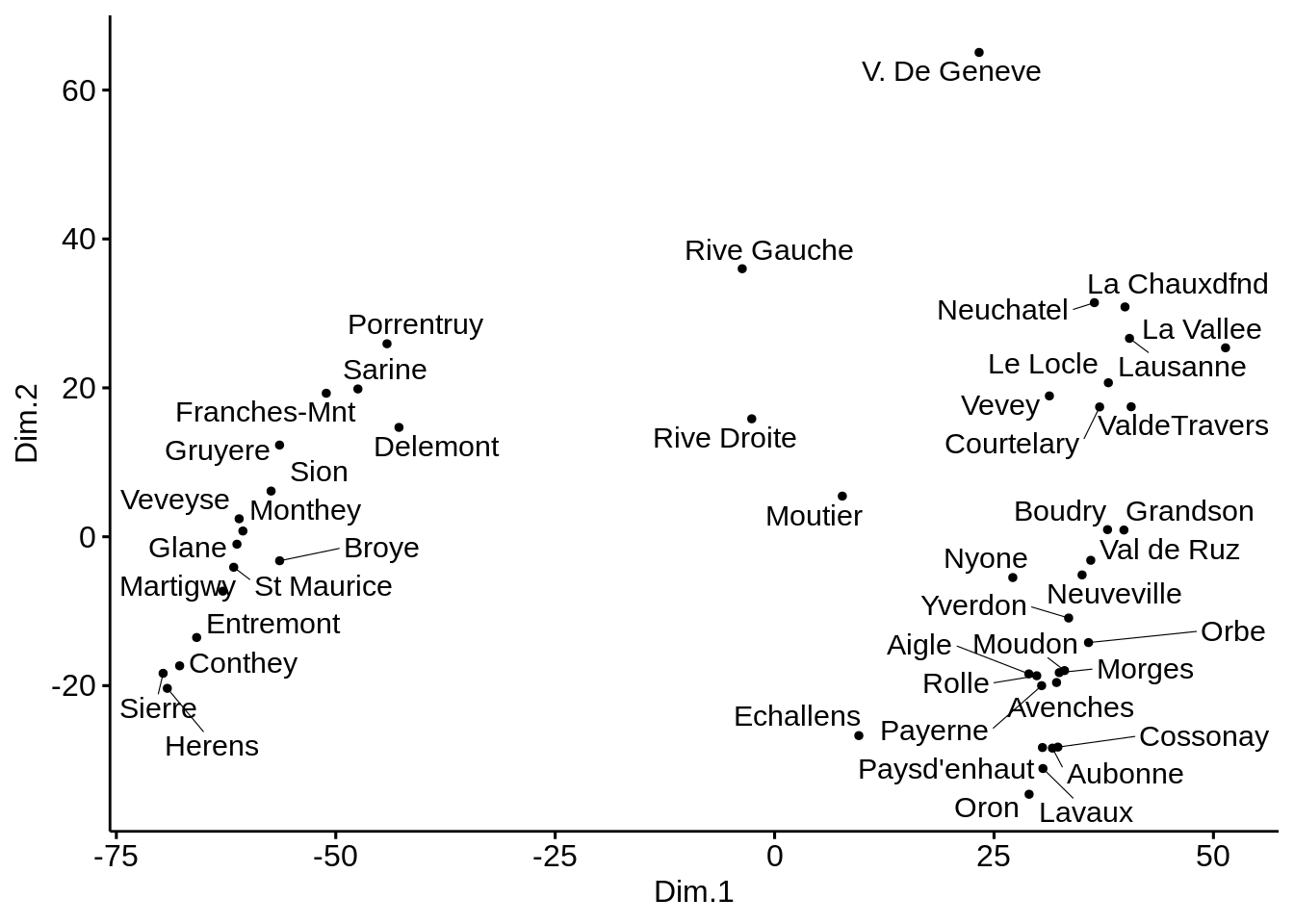

Create \(3\) groups using \(k\)-means clustering and color points by group.

# K-means clustering
clust <- kmeans(mds, 3)$cluster %>%
  as.factor()
mds <- mds %>%
  mutate(groups = clust)
# Plot and color by groups
ggscatter(mds, x = "Dim.1", y = "Dim.2", 
          label = rownames(swiss),
          color = "groups",
          palette = "jco",
          size = 1, 
          ellipse = TRUE,
          ellipse.type = "convex",
          repel = TRUE)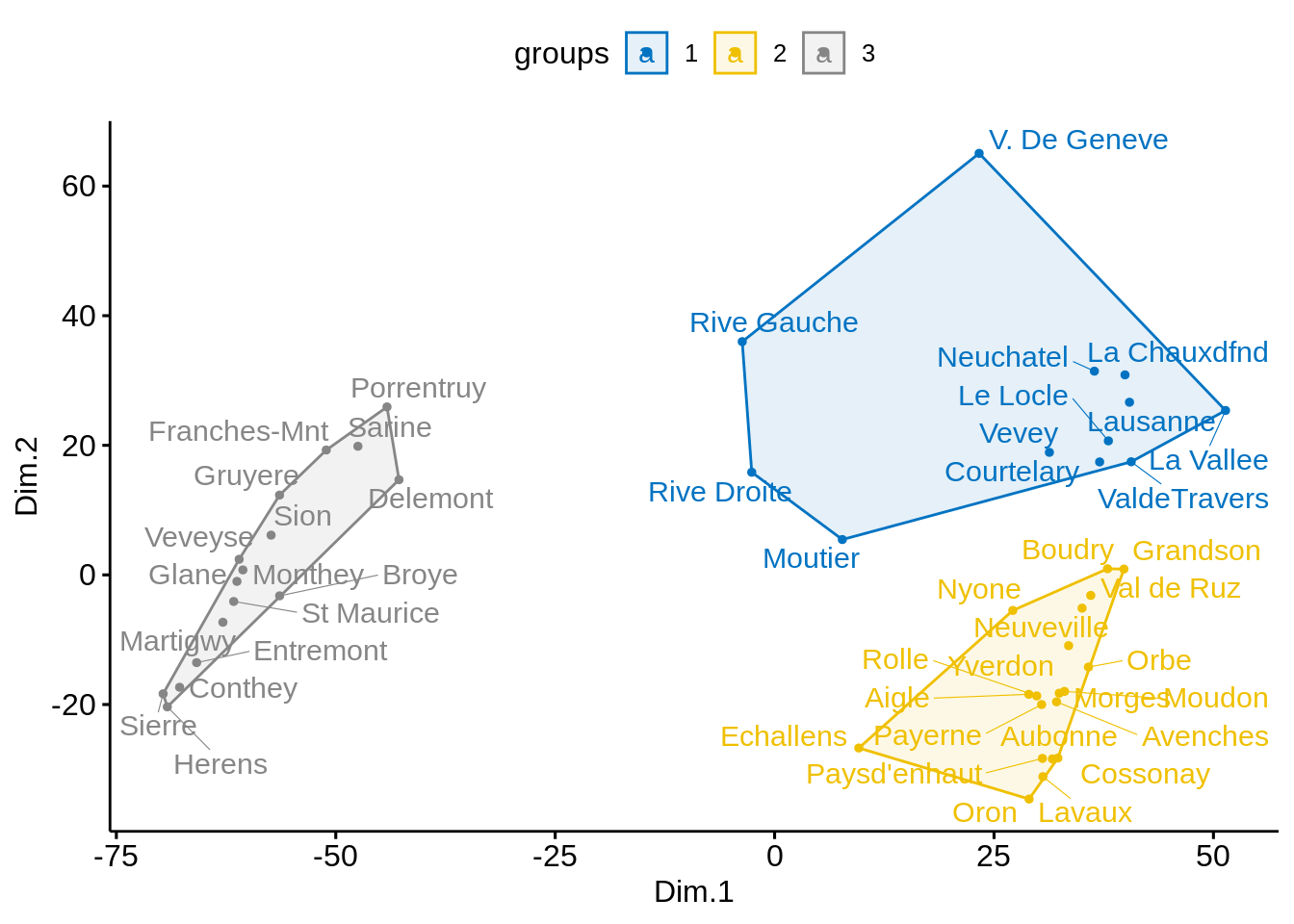

Non-metric MDS

Perform the same analysis with both Kruskal’s non-metric MDS and Sammon’s non-linear mapping. Can you spot any differences?

Kruskal’s non-metric multidimensional scaling

# Cmpute MDS
library(MASS)

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

mds <- swiss %>%
  dist('euclidean') %>%          
  isoMDS() %>%
  .$points %>%
  as_tibble()

## initial  value 5.463800 
## iter   5 value 4.499103
## iter   5 value 4.495335
## iter   5 value 4.492669
## final  value 4.492669 
## converged

colnames(mds) <- c("Dim.1", "Dim.2")


# Plot MDS
ggscatter(mds, x = "Dim.1", y = "Dim.2", 
          label = rownames(swiss),
          size = 1,
          repel = TRUE)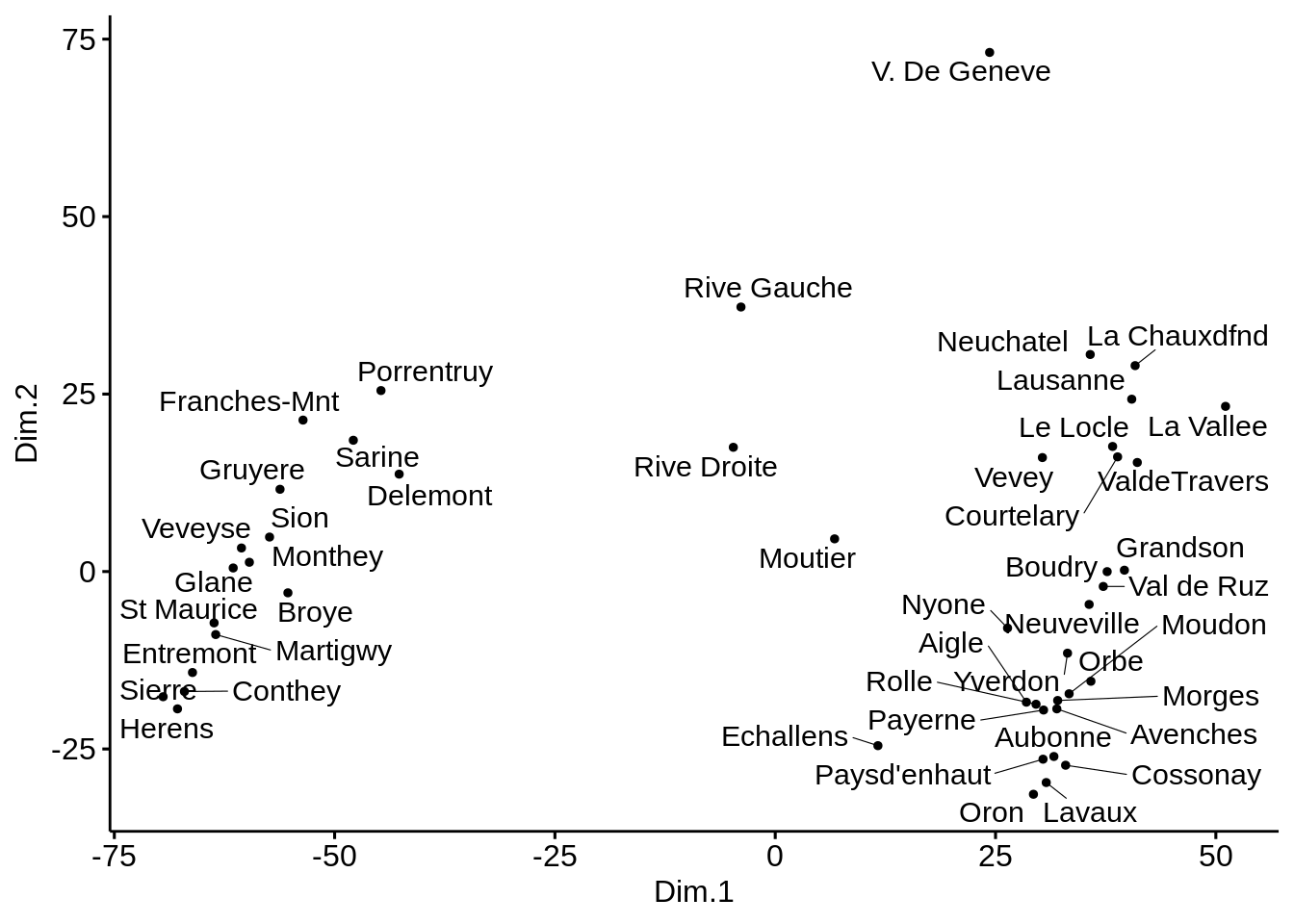

Sammon’s non-linear mapping:

# Cmpute MDS
library(MASS)
mds <- swiss %>%
  dist() %>%          
  sammon() %>%
  .$points %>%
  as_tibble()

## Initial stress        : 0.01959
## stress after   0 iters: 0.01959

colnames(mds) <- c("Dim.1", "Dim.2")

# Plot MDS
ggscatter(mds, x = "Dim.1", y = "Dim.2", 
          label = rownames(swiss),
          size = 1,
          repel = TRUE)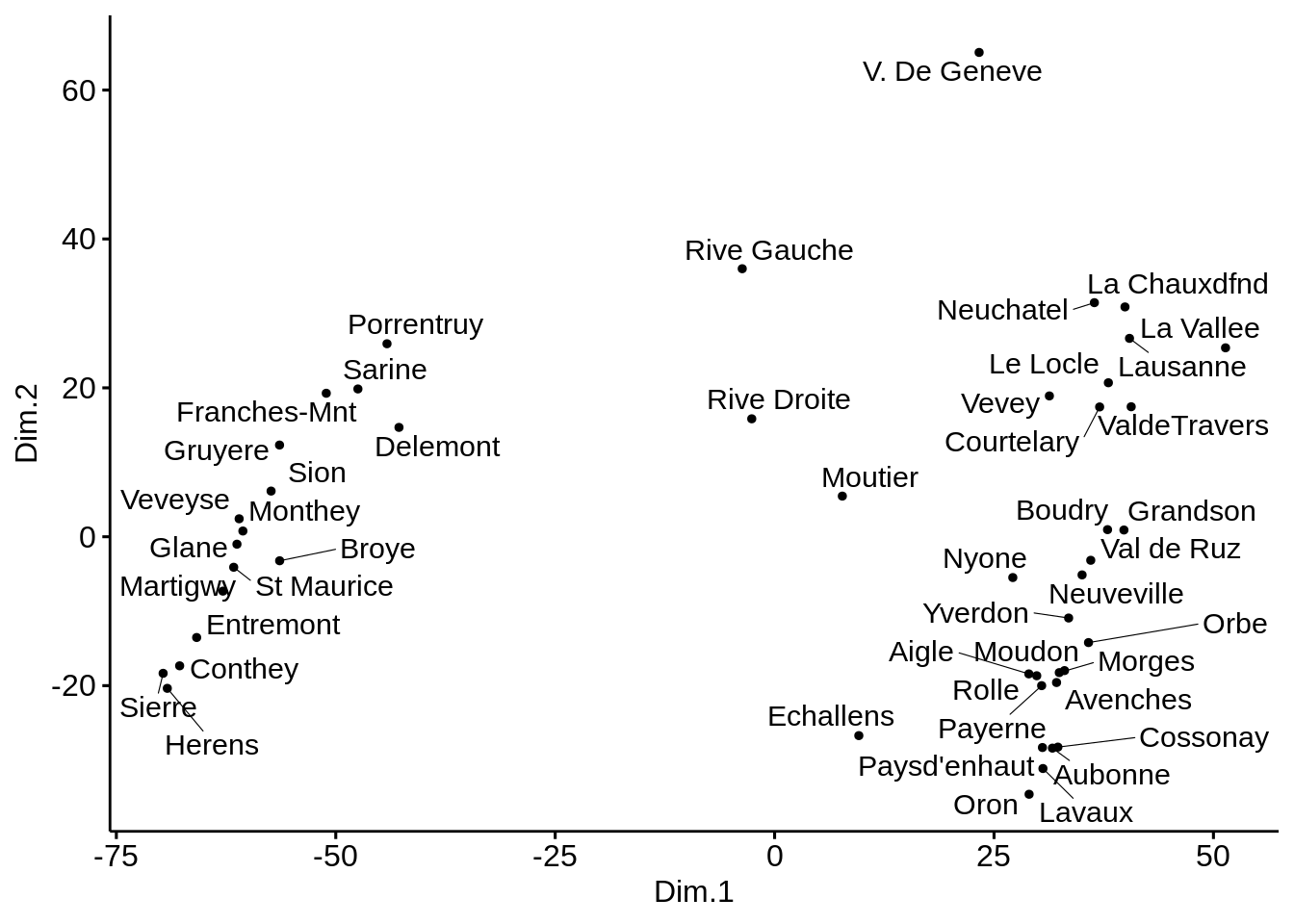

Here, there does not seem to be much difference between all methods. This is probably due to the fact that we are always using the ‘Euclidian’ distance.

Correlation matrix using Multidimensional Scaling

MDS can also be used to detect a hidden pattern in a correlation matrix.

res.cor <- cor(mtcars, method = "spearman")
res.cor

##             mpg        cyl       disp         hp        drat         wt
## mpg   1.0000000 -0.9108013 -0.9088824 -0.8946646  0.65145546 -0.8864220
## cyl  -0.9108013  1.0000000  0.9276516  0.9017909 -0.67888119  0.8577282
## disp -0.9088824  0.9276516  1.0000000  0.8510426 -0.68359210  0.8977064
## hp   -0.8946646  0.9017909  0.8510426  1.0000000 -0.52012499  0.7746767
## drat  0.6514555 -0.6788812 -0.6835921 -0.5201250  1.00000000 -0.7503904
## wt   -0.8864220  0.8577282  0.8977064  0.7746767 -0.75039041  1.0000000
## qsec  0.4669358 -0.5723509 -0.4597818 -0.6666060  0.09186863 -0.2254012
## vs    0.7065968 -0.8137890 -0.7236643 -0.7515934  0.44745745 -0.5870162
## am    0.5620057 -0.5220712 -0.6240677 -0.3623276  0.68657079 -0.7377126
## gear  0.5427816 -0.5643105 -0.5944703 -0.3314016  0.74481617 -0.6761284
## carb -0.6574976  0.5800680  0.5397781  0.7333794 -0.12522294  0.4998120
##             qsec         vs          am       gear        carb
## mpg   0.46693575  0.7065968  0.56200569  0.5427816 -0.65749764
## cyl  -0.57235095 -0.8137890 -0.52207118 -0.5643105  0.58006798
## disp -0.45978176 -0.7236643 -0.62406767 -0.5944703  0.53977806
## hp   -0.66660602 -0.7515934 -0.36232756 -0.3314016  0.73337937
## drat  0.09186863  0.4474575  0.68657079  0.7448162 -0.12522294
## wt   -0.22540120 -0.5870162 -0.73771259 -0.6761284  0.49981205
## qsec  1.00000000  0.7915715 -0.20333211 -0.1481997 -0.65871814
## vs    0.79157148  1.0000000  0.16834512  0.2826617 -0.63369482
## am   -0.20333211  0.1683451  1.00000000  0.8076880 -0.06436525
## gear -0.14819967  0.2826617  0.80768800  1.0000000  0.11488698
## carb -0.65871814 -0.6336948 -0.06436525  0.1148870  1.00000000

head(mtcars)

##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

Would you say that correlation is a measure of similarity or dissimilarity? Using correlation, how would you compute distances between objects

Correlation actually measures similarity, but it is easy to transform it to a measure of dissimilarity. Distance between objects can be calculated as 1 - res.cor.

Perform a classical MDS on the mtcars dataset and comment.

mds.cor <- (1 - res.cor) %>%
  cmdscale() %>%
  as_tibble()
colnames(mds.cor) <- c("Dim.1", "Dim.2")
ggscatter(mds.cor, x = "Dim.1", y = "Dim.2", 
          size = 1,
          label = colnames(res.cor),
          repel = TRUE)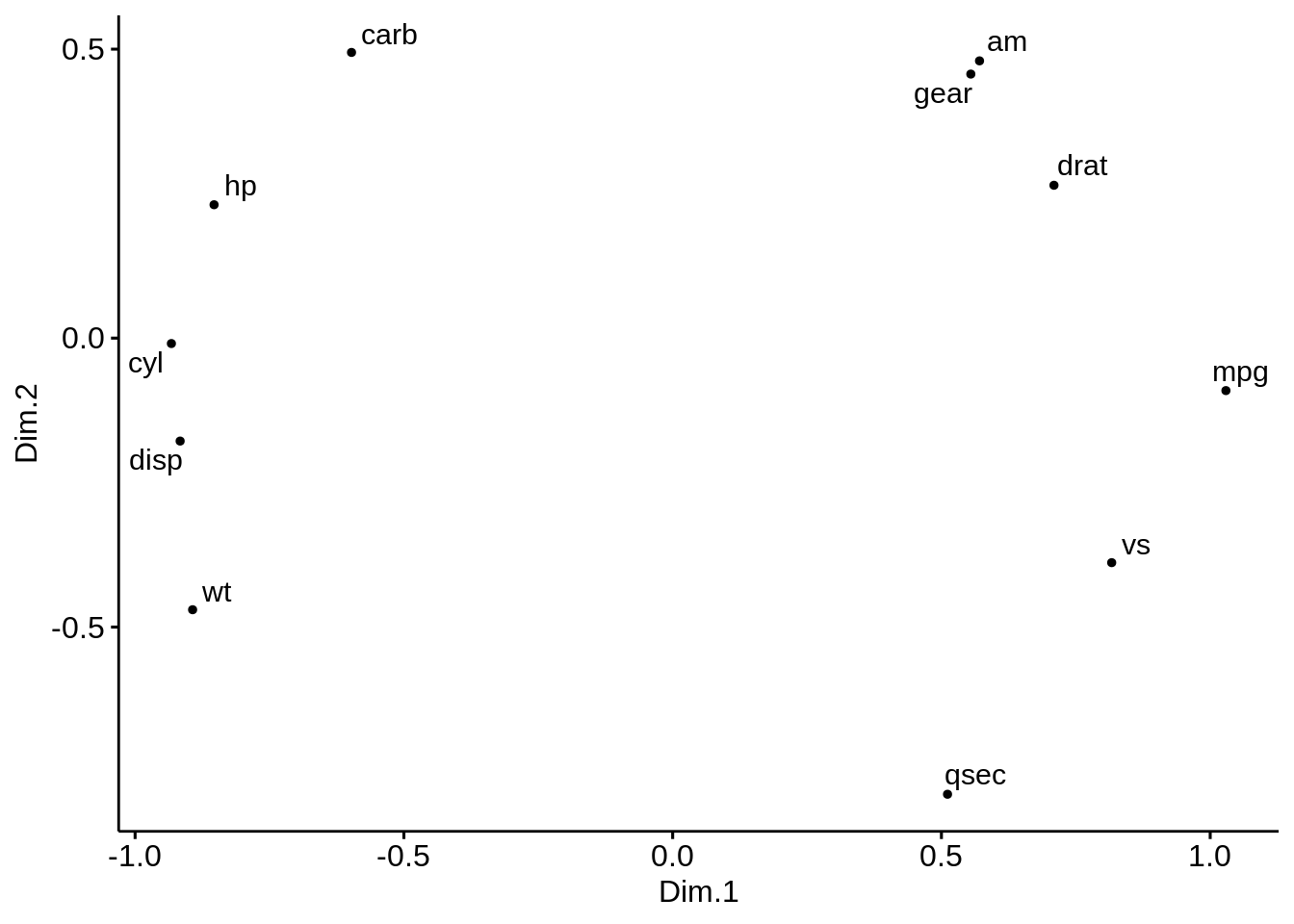

Observe here that we are performing the MDS on the variables rather on the individuals. Positive correlated objects are close together on the same side of the plot.

Perform a PCA on the mtcars dataset. Comment on the differences with MDS. Recall what are the main differences between MDS and PCA

pca <- FactoMineR::PCA(mtcars)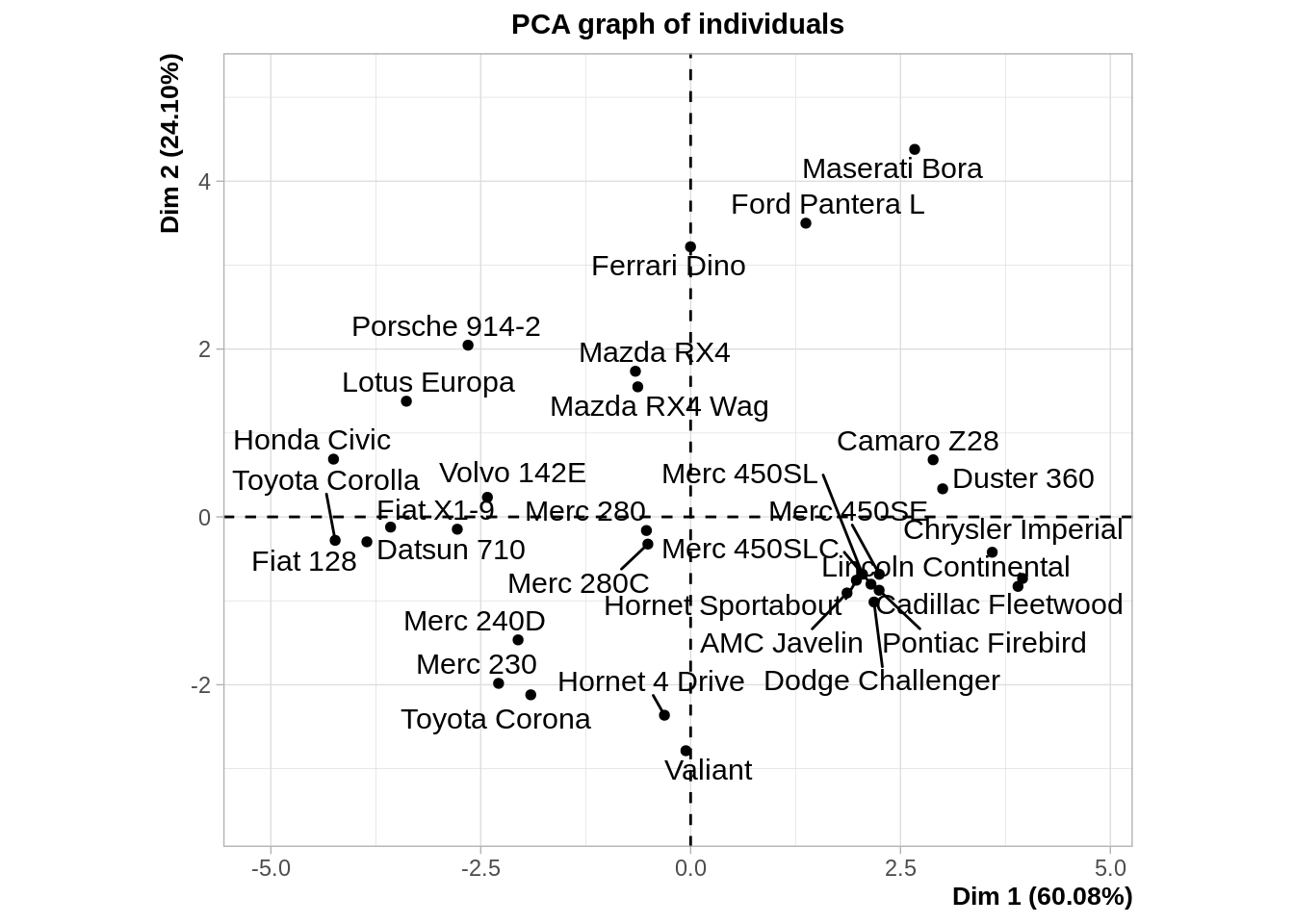

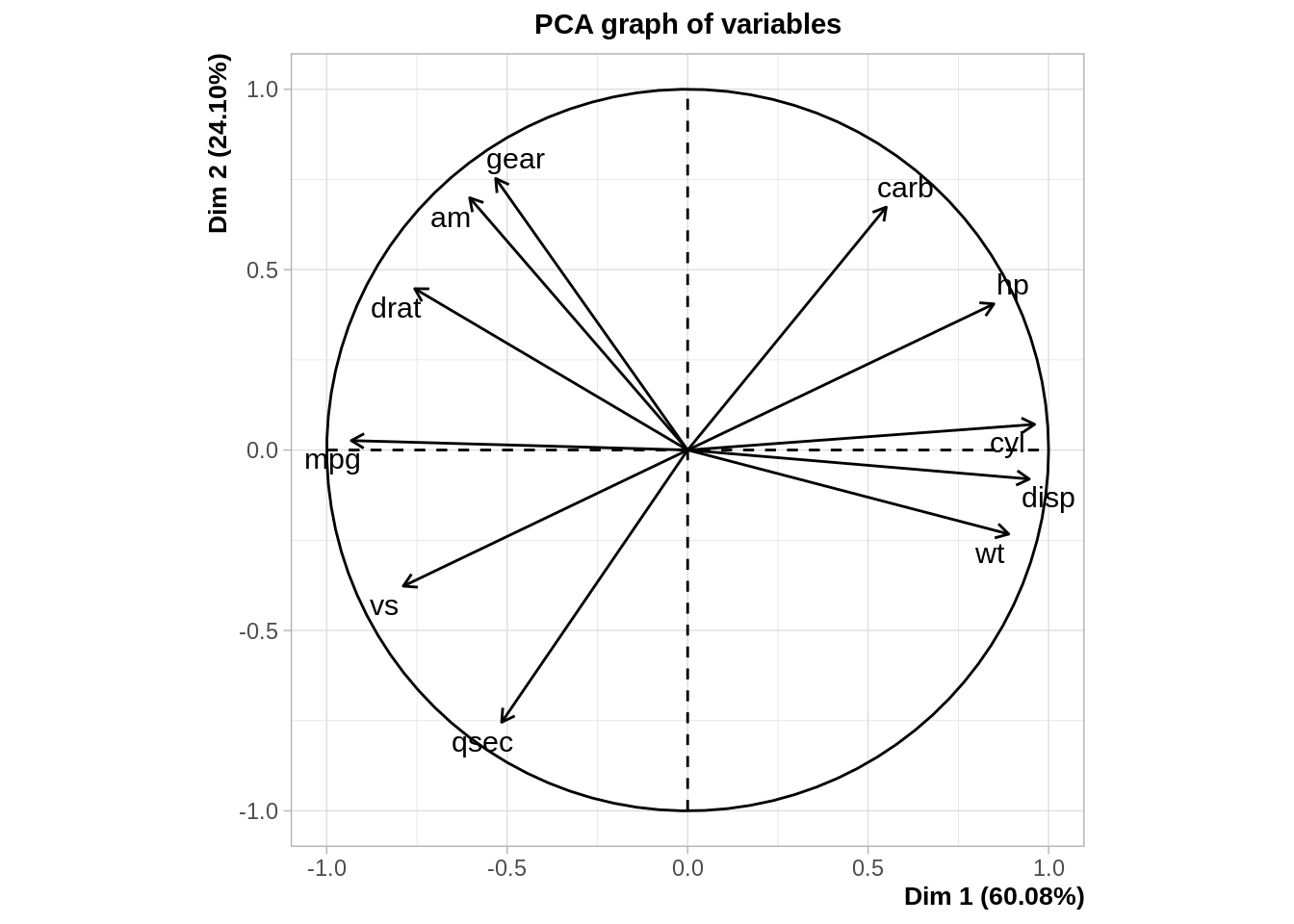
MDS and PCA are equivalent when considering classical scaling and Euclidean distances.

Mathematically and conceptually, there are close correspondences between MDS and other methods used to reduce the dimensionality of complex data, such as Principal components analysis (PCA) and factor analysis.

PCA is more focused on the dimensions themselves, and seek to maximize explained variance, whereas MDS is more focused on relations among the scaled objects.

MDS projects n-dimensional data points to a (commonly) 2-dimensional space such that similar objects in the n-dimensional space will be close together on the two dimensional plot, while PCA projects a multidimensional space to the directions of maximum variability using covariance/correlation matrix to analyze the correlation between data points and variables.

Pairwise distances between American cities

The UScitiesD dataset gives ‘straight line’ distances between \(10\) cities in the US.

?UScitiesD
cities <- UScitiesD
cities

##               Atlanta Chicago Denver Houston LosAngeles Miami NewYork
## Chicago           587                                                
## Denver           1212     920                                        
## Houston           701     940    879                                 
## LosAngeles       1936    1745    831    1374                         
## Miami             604    1188   1726     968       2339              
## NewYork           748     713   1631    1420       2451  1092        
## SanFrancisco     2139    1858    949    1645        347  2594    2571
## Seattle          2182    1737   1021    1891        959  2734    2408
## Washington.DC     543     597   1494    1220       2300   923     205
##               SanFrancisco Seattle
## Chicago                           
## Denver                            
## Houston                           
## LosAngeles                        
## Miami                             
## NewYork                           
## SanFrancisco                      
## Seattle                678        
## Washington.DC         2442    2329

Just looking at the table does not provide any information about the underlying structure of the data (i.e. the position of each city on a map). We are going to apply MDS to recover the geographical structure.

Run the following code which displays the US map with the \(10\) cities we are considering.

names <- c("Atlanta GA", "Chicago IL", "Denver CO", "Houston TX", 
                    "Los Angeles CA", "Miami FL", "New York NY", "San Francisco CA",                                          "Seattle WA", "WASHINGTON DC")
df <- tibble::as_tibble(us.cities)
df <- df %>% filter(name %in% names)

usa <- map_data("usa")
gg1 <- ggplot() + 
  geom_polygon(data = usa, aes(x=long, y = lat, group = group), fill = "NA", color = "blue") + 
  coord_fixed(1.3)

labs <- data.frame(
  long = df$long,
  lat = df$lat,
  names = df$name,
  stringsAsFactors = FALSE
  )  

gg1 + 
  geom_point(data = labs, aes(x = long, y = lat), color = "black", size = 5) +
  geom_point(data = labs, aes(x = long, y = lat), color = "yellow", size = 4) + 
  geom_text_repel(data = labs, aes(x=long , y=lat, label = names), size=3)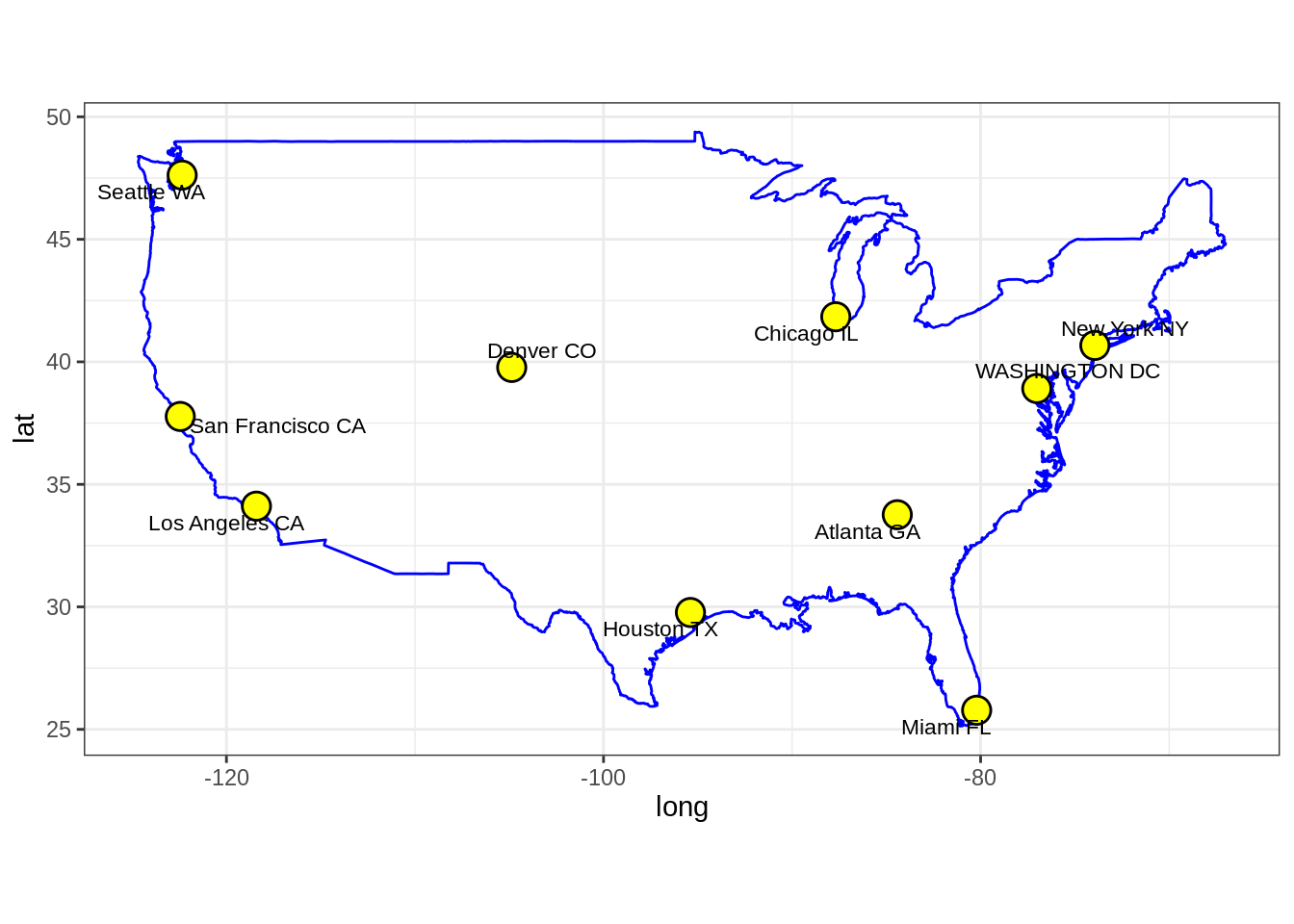

Plot the MDS representation of the pair-wise distances for the \(10\) US cities. Comment on the results. Is this the usual US map? Does this somehow contradict the use of MDS for dimensionality reduction?

cities_mds <- cities %>%
  cmdscale() %>%
  scale() %>% 
  as_tibble()

colnames(cities_mds) <- c("Dim.1", "Dim.2")
us.cities.name <- c("Atlanta", "Chicago", "Denver", "Houston", 
                    "LA", "Miami", "NYC", "SF", "Seattle", "DC")

cities_mds_rev <- cities_mds
cities_mds_rev$Dim.1 <- -cities_mds$Dim.1
cities_mds_rev$Dim.2 <- -cities_mds$Dim.2


ggscatter(cities_mds, x = "Dim.1", y = "Dim.2", 
          label = us.cities.name,
          size = 1,
          repel = TRUE)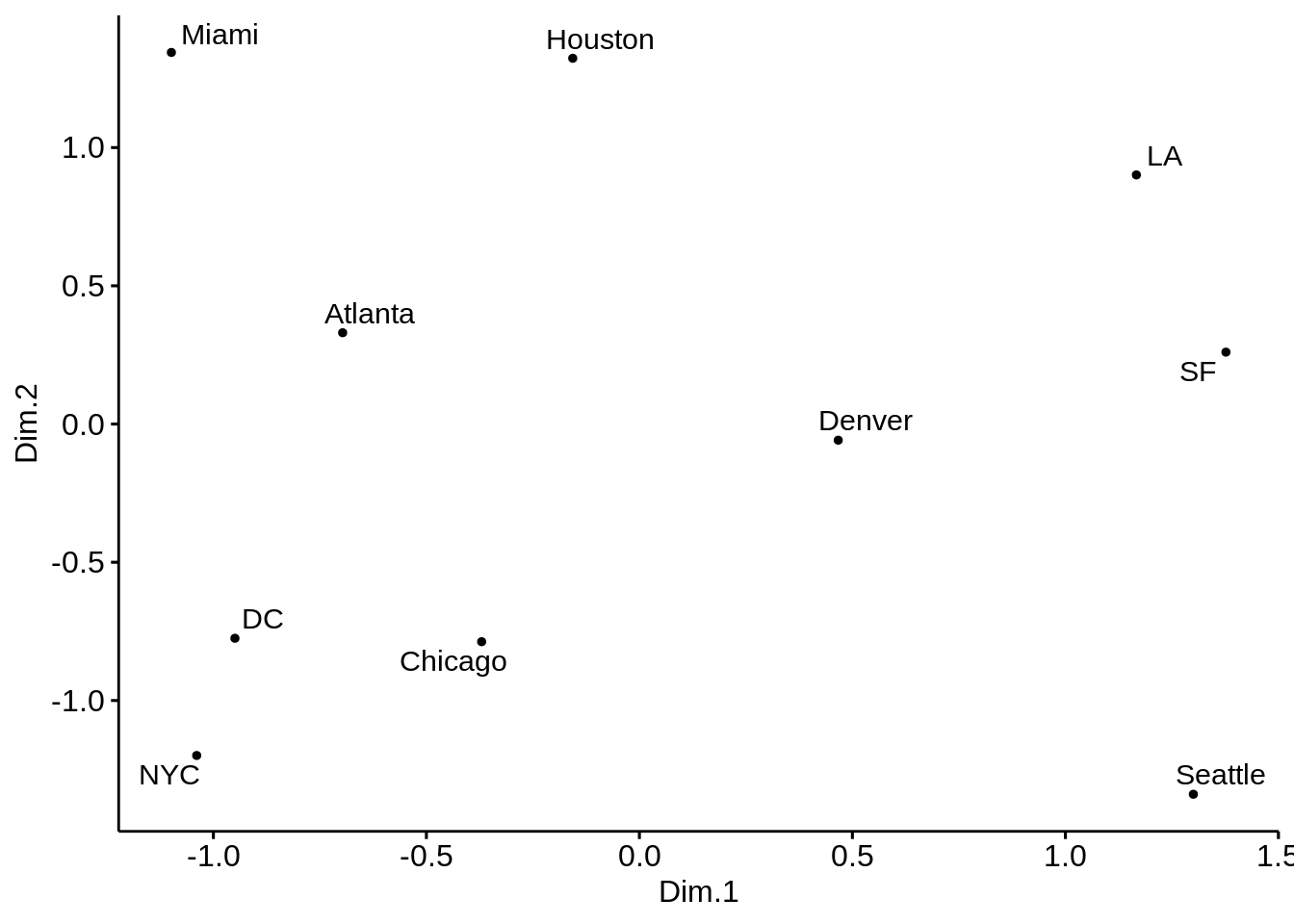

ggscatter(cities_mds_rev, x = "Dim.1", y = "Dim.2", 
          label = us.cities.name,
          size = 1,
          repel = TRUE)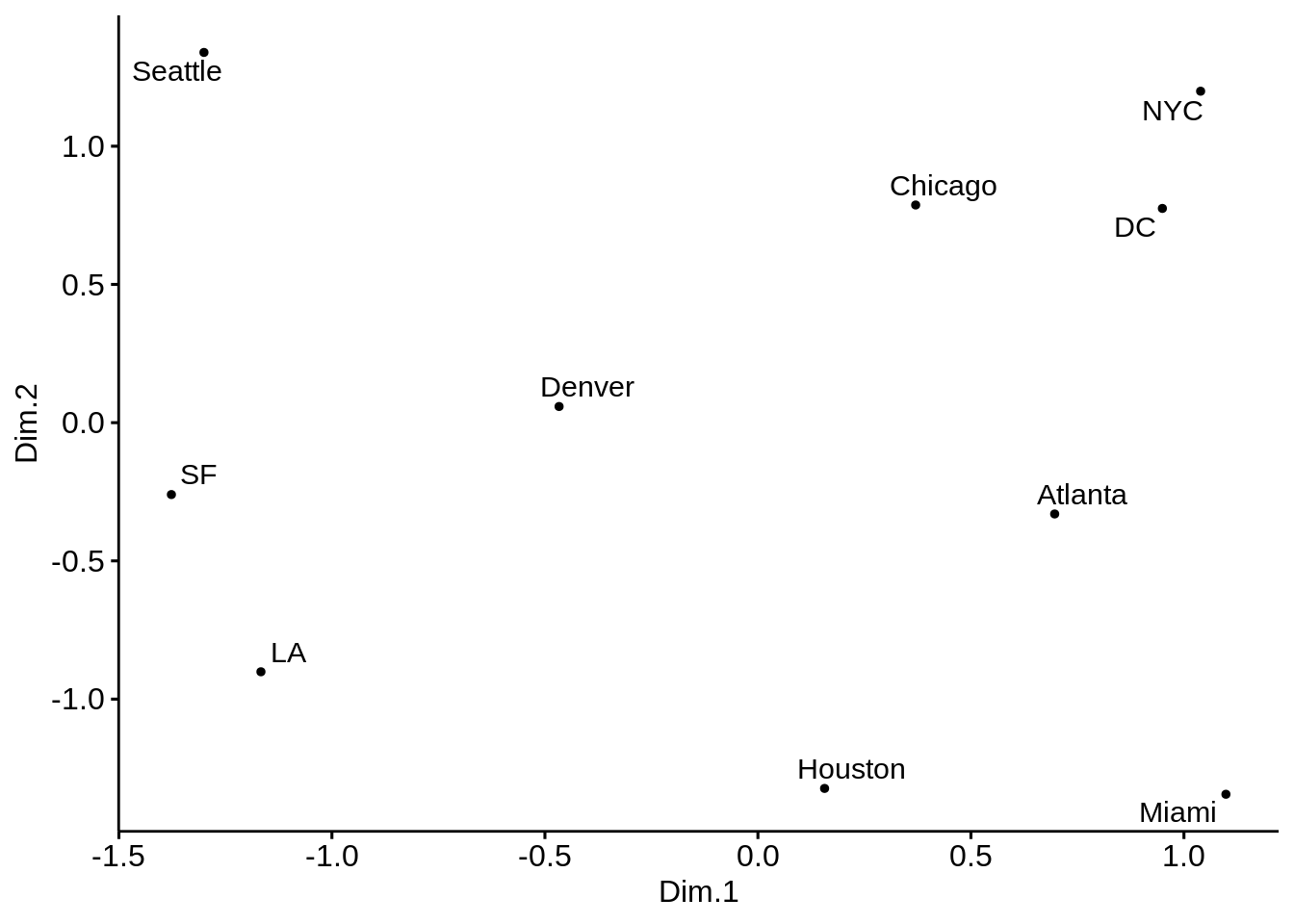

#solution 2 (with ggplot)
p <- ggplot(data = cities_mds) + geom_point(mapping = aes(x=Dim.1 , y=Dim.2), color="yellow", size=8)
p <- p + geom_text(data = cities_mds, mapping = aes(x=Dim.1 , y=Dim.2), label = us.cities.name, size=3)
p <- p + labs(title = "MDS representation of pair-wise distances of 21 European cities")
p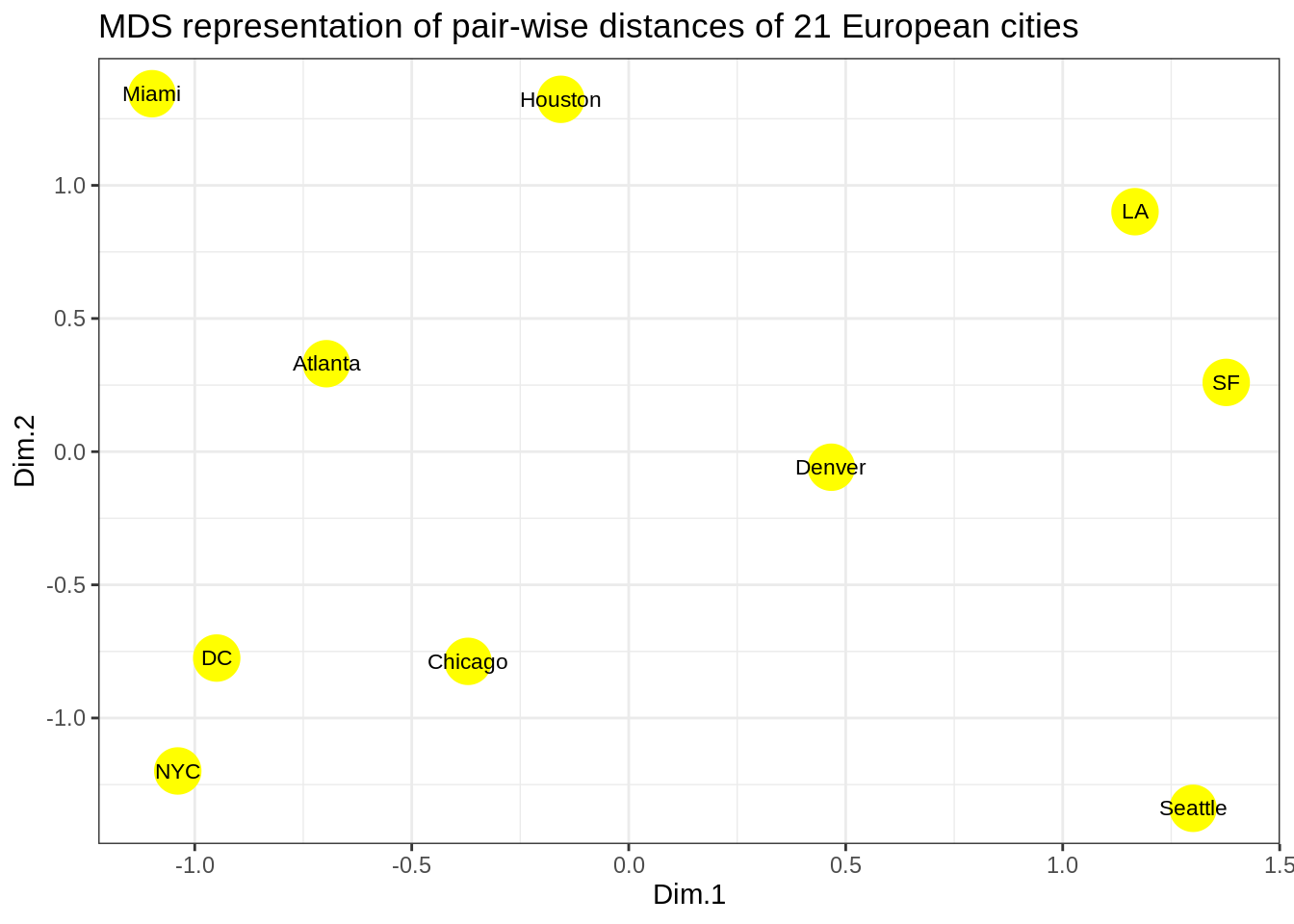

The cities on the map are not in their expected locations. It seems the map is not only mirrored, but flipped (Australia’s point of view). Indeed, this is the proper time to point to the fact that MDS only tries to preserve the inter-object distances, and therefore there is nothing wrong with the map. By operations such as rotation of the map, the distances remain intact. The map must be rotated 180 degrees. It is possible to do so by multiplying the coordinates of each point into -1.

Solve the issue above by rotating the figure the proper way.

p <- ggplot(data = cities_mds) + geom_point(mapping = aes(x=-Dim.1 , y=-Dim.2), color="yellow", size=8)
p <- p + geom_text(data = cities_mds, mapping = aes(x=-Dim.1 , y=-Dim.2), label = us.cities.name, size=3)
p <- p + labs(title = "MDS representation of pair-wise distances of 21 European cities")
p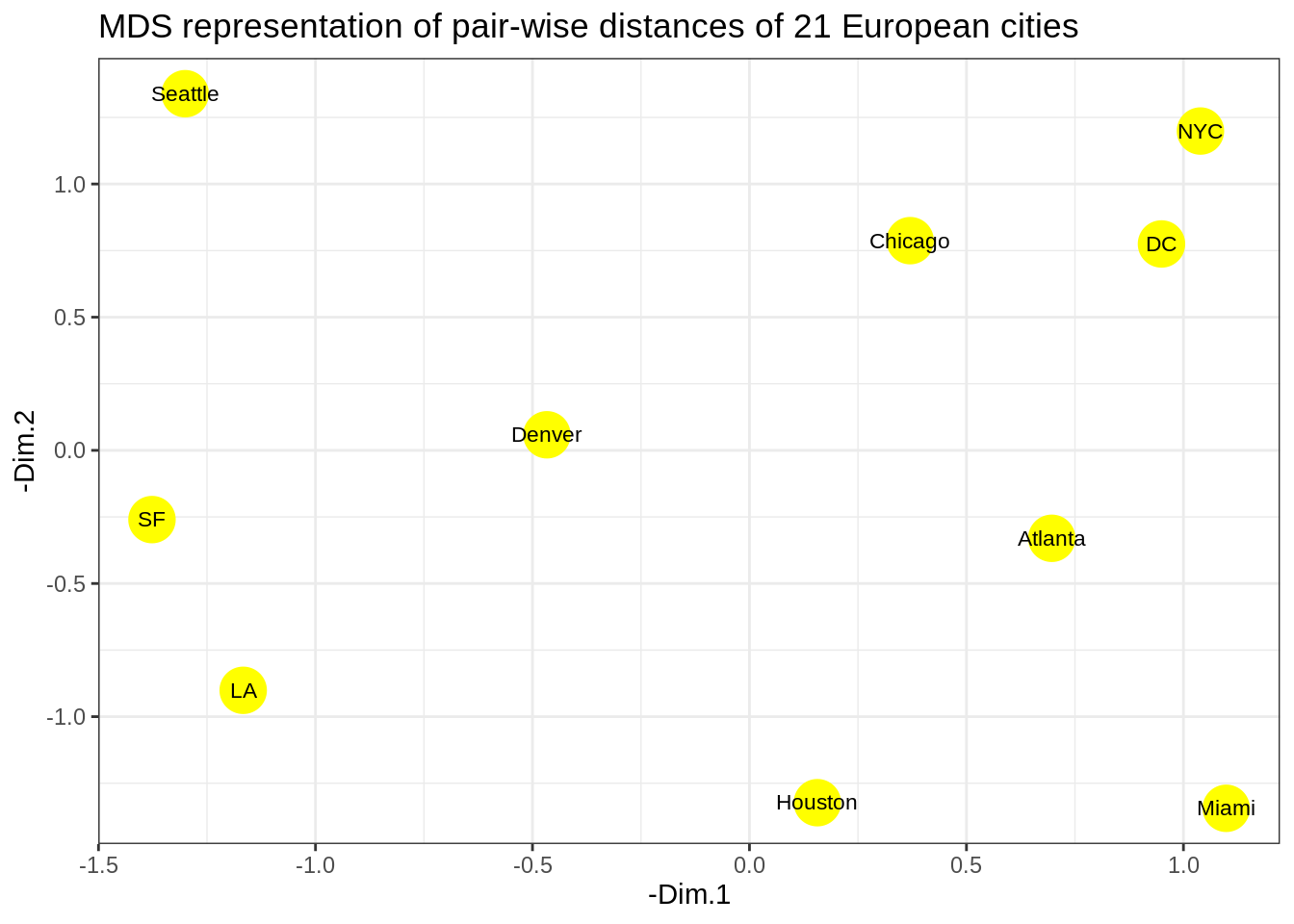

Kernel PCA

Reminders

Recall that the principal components variables \(Z\) of a data matrix \(X\) can be computed from the inner-product (gram) matrix \(K=XX^\top\). In detail, we compute the eigen-decomposition of the double-centered version of the gram matrix \[ \tilde{K} = (I-M) K (I-M) = U D^2 U^\top, \] where \(M = \frac 1n \mathbf{1}\mathbf{1}^\top\) and \(Z = UD\). Kernel PCA mimics this proceduren interpreting the kernel matrix \(\mathbf K = (K(x_i,x_{i^{'}}))_{1 \leq i,i^{'} \leq n}\) as an inner-product matrix of the implicit features \(\langle \phi(x_i), \phi(x_{i^{'}}) \rangle\) and finding its eigen vectors.

With Python using reticulate in R

library(reticulate)
reticulate::use_virtualenv("r-reticulate")
reticulate::py_config()

## python:         /usr/share/miniconda/envs/MAP573/bin/python3
## libpython:      /usr/share/miniconda/envs/MAP573/lib/libpython3.7m.so
## pythonhome:     /usr/share/miniconda/envs/MAP573:/usr/share/miniconda/envs/MAP573
## version:        3.7.8 | packaged by conda-forge | (default, Jul 31 2020, 02:25:08)  [GCC 7.5.0]
## numpy:          /usr/share/miniconda/envs/MAP573/lib/python3.7/site-packages/numpy
## numpy_version:  1.19.4
## umap:           [NOT FOUND]
## 
## python versions found: 
##  /usr/share/miniconda/envs/MAP573/bin/python3
##  /usr/bin/python3
##  /usr/bin/python

# py_install("sklearn"   , pip=TRUE) # you need to install package sklearn first time
# py_install("matplotlib", pip=TRUE) # you need to install install matplotlib first time

Let us start with a simple example of the two half-moon shapes generated by the make_moons functions from sklearn_learn.

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, random_state=123)

plt.figure(figsize=(8,6))

plt.scatter(X[y==0, 0], X[y==0, 1], color='red', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', alpha=0.5)

plt.title('A nonlinear 2Ddataset')
plt.ylabel('y coordinate')
plt.xlabel('x coordinate')

plt.show()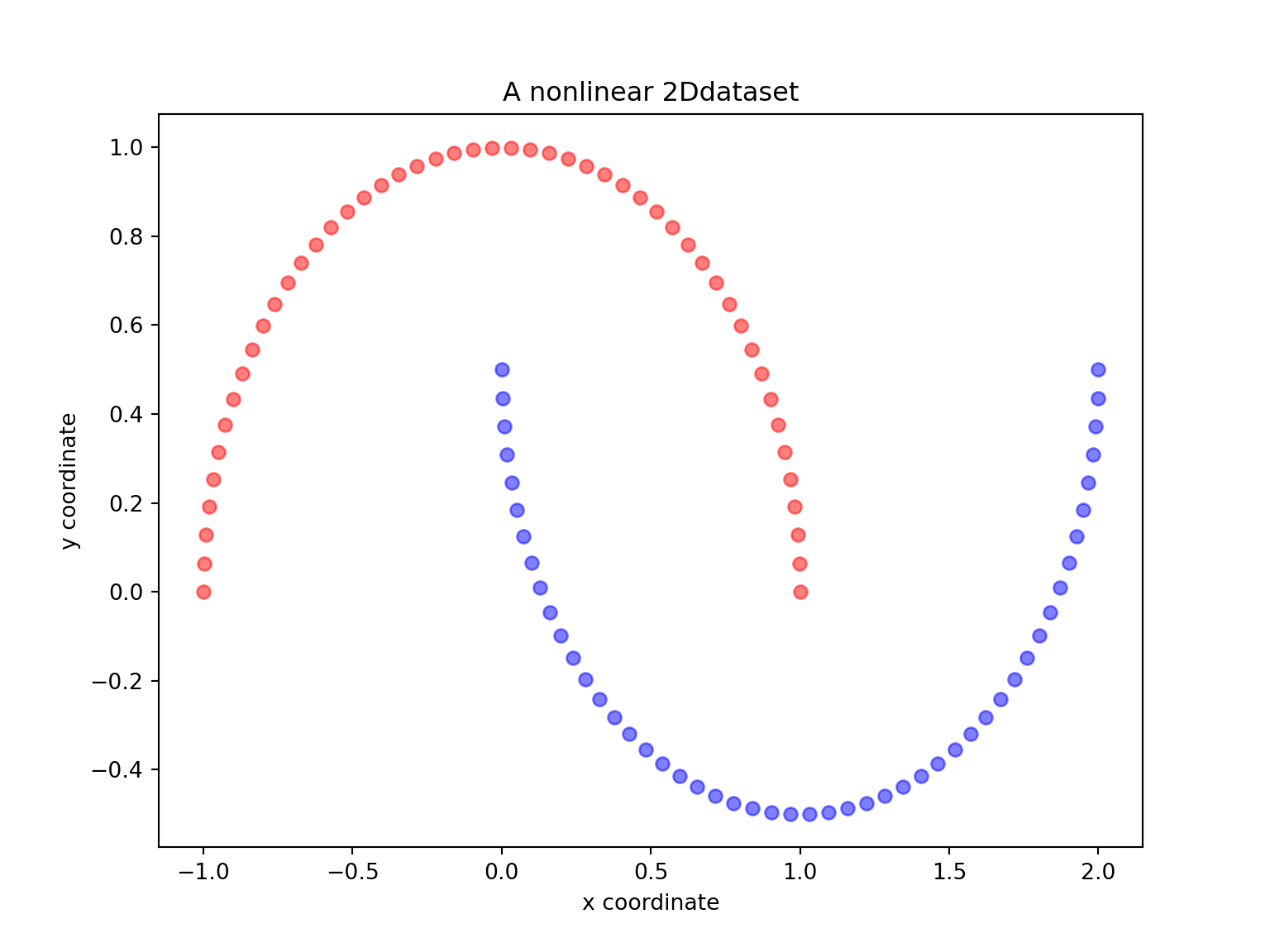

Are the two half-moon shapes linearly separable? Do you expect PCA to give satisfactory results? Perform a PCA using sklearn with n_components \(=1\) and \(2\). Comment.

from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import numpy as np

X, y = make_moons(n_samples=100, random_state=123)

#PCA with n_components = 1
scikit_pca = PCA(n_components=1)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_spca[y==0, 0], np.zeros((50,1)), color='red', alpha=0.5)
plt.scatter(X_spca[y==1, 0], np.zeros((50,1)), color='blue', alpha=0.5)

plt.title('First principal component after Linear PCA')
plt.xlabel('PC1')

plt.show()

#PCA with n_components = 2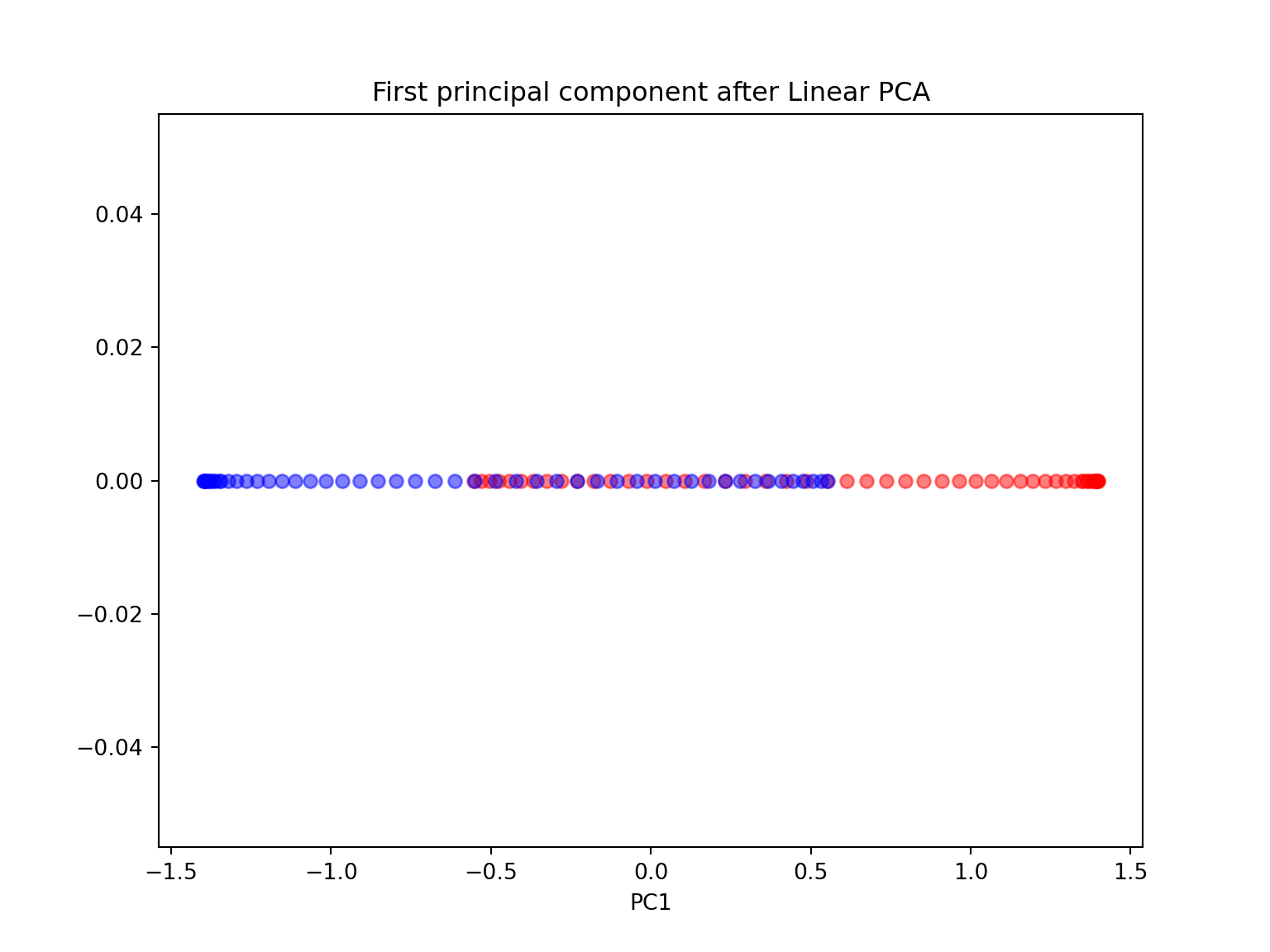

scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_spca[y==0, 0], X_spca[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_spca[y==1, 0], X_spca[y==1, 1], color='blue', alpha=0.5)

plt.title('First 2 principal component after Linear PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')

plt.show()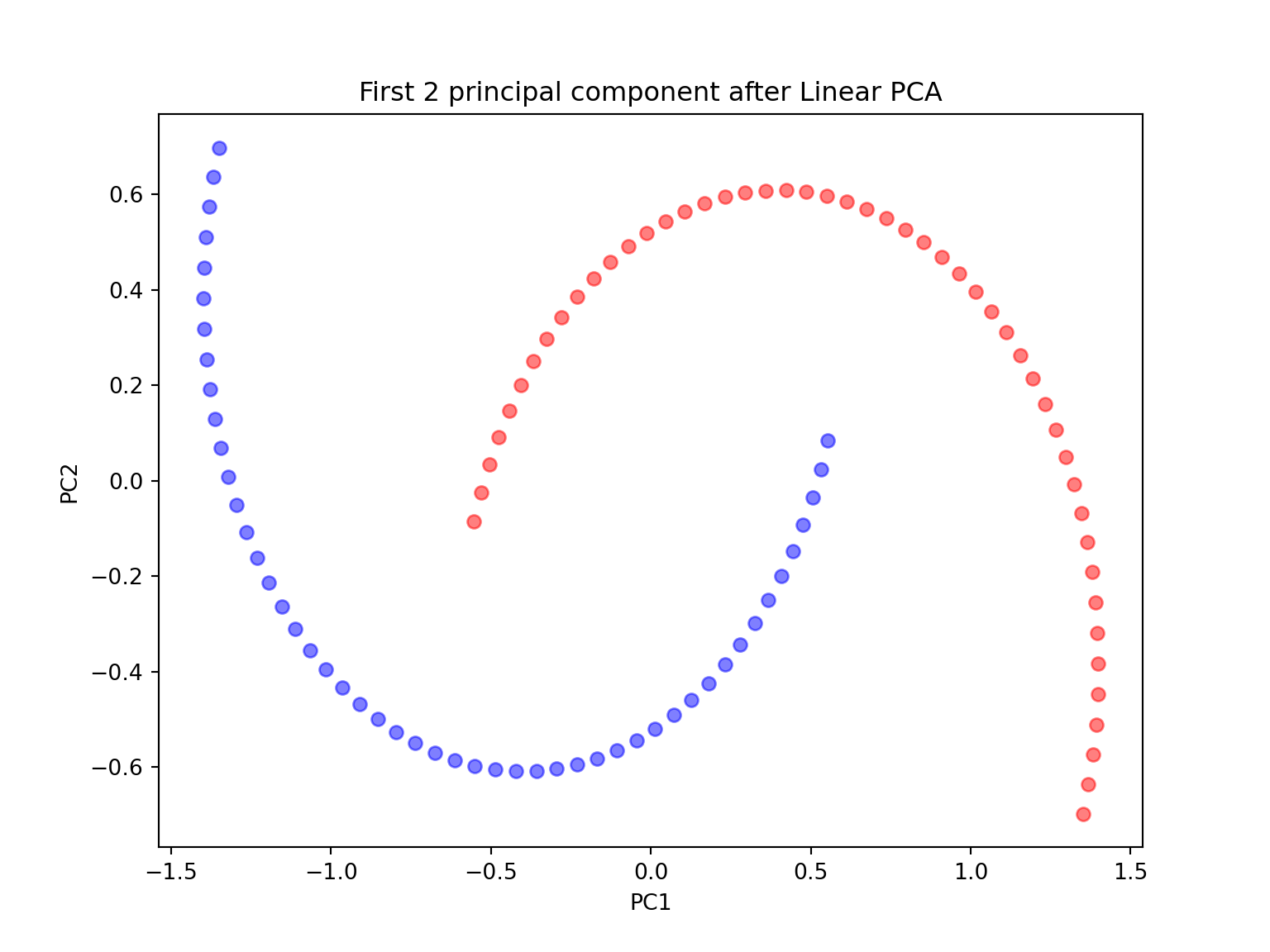

Since the two half-moon shapes are linearly inseparable, we expect the ‘classic’ PCA to fail giving us a ‘good’ representation of the data in 1D space. As we can see, the resulting principal components do not yield a subspace where the data is linearly separated well.

Perform a KernelPCA using the KernelPCA function from sklearn with the rbf kernel and \(\gamma=15\) with both n_components \(=1\) and \(2\). Comment. Try different values for \(\gamma\) and different kernels. Comment.

from sklearn.decomposition import KernelPCA
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
import numpy as np

#kernel PCA with n_components = 1

gamma = 15
X, y = make_moons(n_samples=100, random_state=123)
X_pc = KernelPCA(gamma=15, n_components=1, kernel='rbf').fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_pc[y==0, 0], np.zeros((50,1)), color='red', alpha=0.5)
plt.scatter(X_pc[y==1, 0], np.zeros((50,1)), color='blue', alpha=0.5)

plt.title('First principal components after RBF Kernel PCA with $\gamma$={}'.format(gamma))
plt.xlabel('PC1')
plt.show()

#kernel PCA with n_components = 2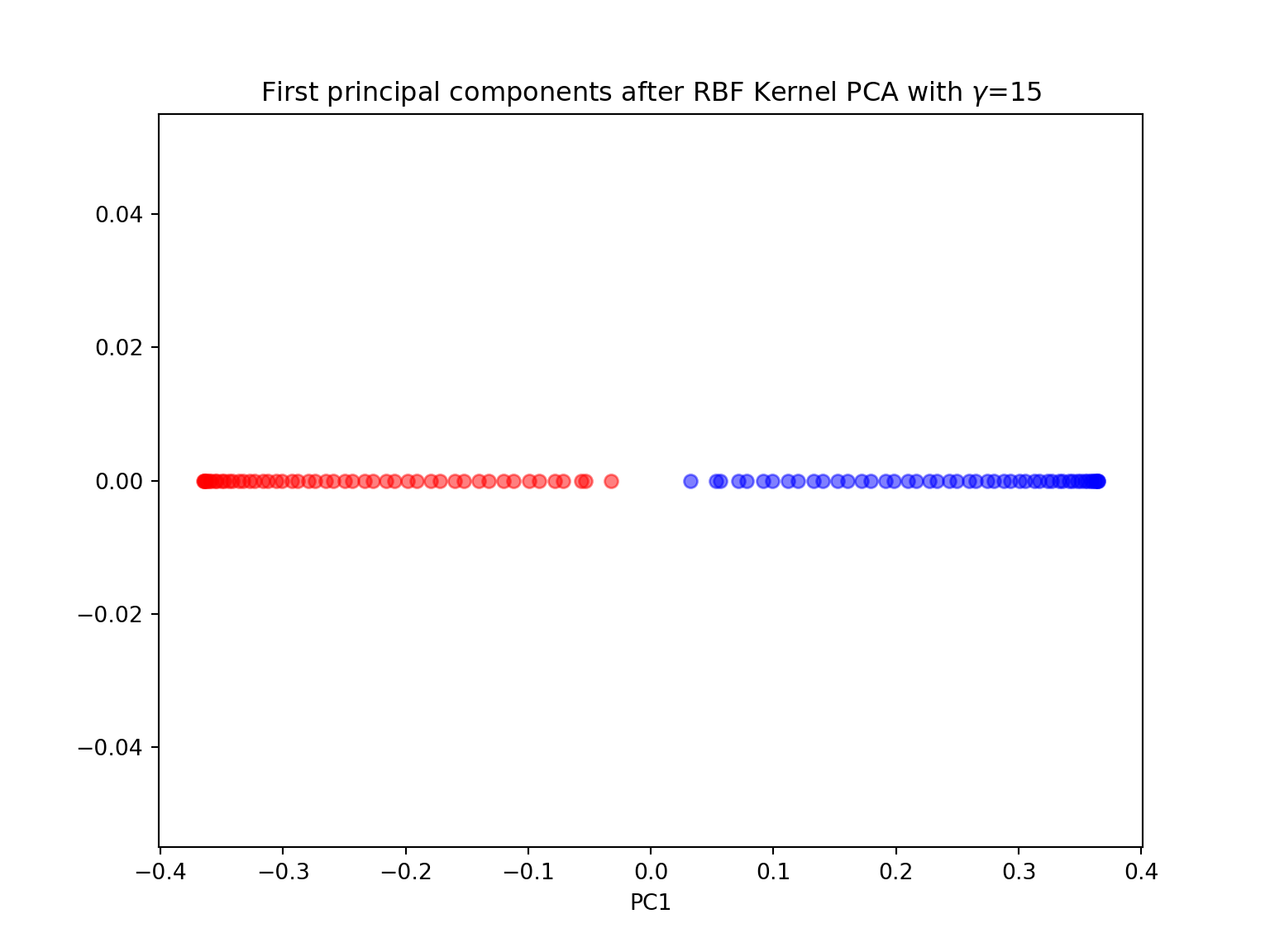

X_pc = KernelPCA(gamma=15, n_components=2, kernel='rbf').fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_pc[y==0, 0], X_pc[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_pc[y==1, 0], X_pc[y==1, 1], color='blue', alpha=0.5)

plt.title('First 2 principal components after RBF Kernel PCA with $\gamma$={}'.format(gamma))
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()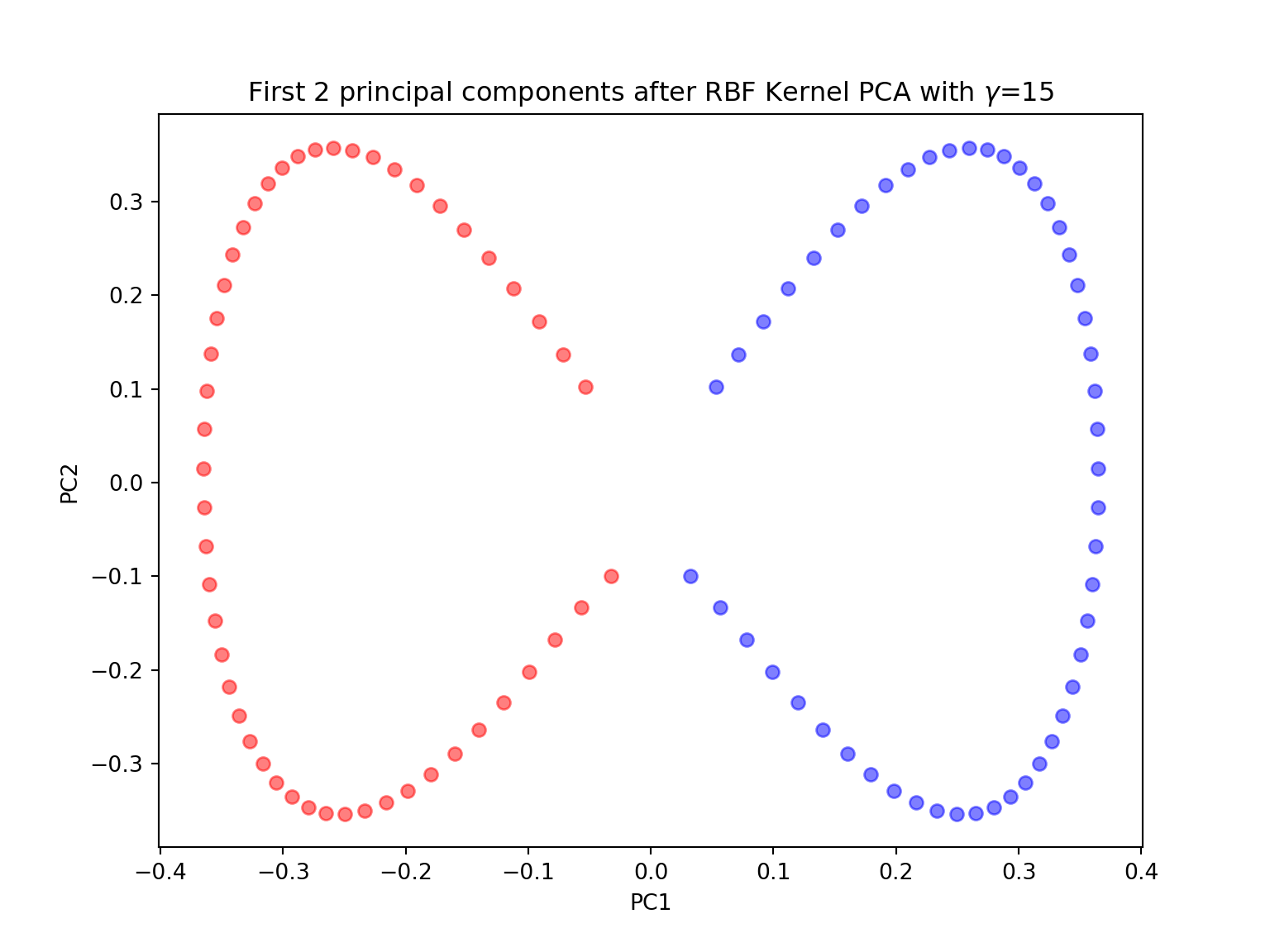

Concentric circles

Another well-known example for which linear PCA will fail is the classic case of two concentric circles with random noise: have a look at make_circles.

from sklearn.datasets import make_circles
import matplotlib.pyplot as plt
import numpy as np

X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)

plt.figure(figsize=(8,6))

plt.scatter(X[y==0, 0], X[y==0, 1], color='red', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', alpha=0.5)
plt.title('Concentric circles')
plt.ylabel('y coordinate')
plt.xlabel('x coordinate')
plt.show()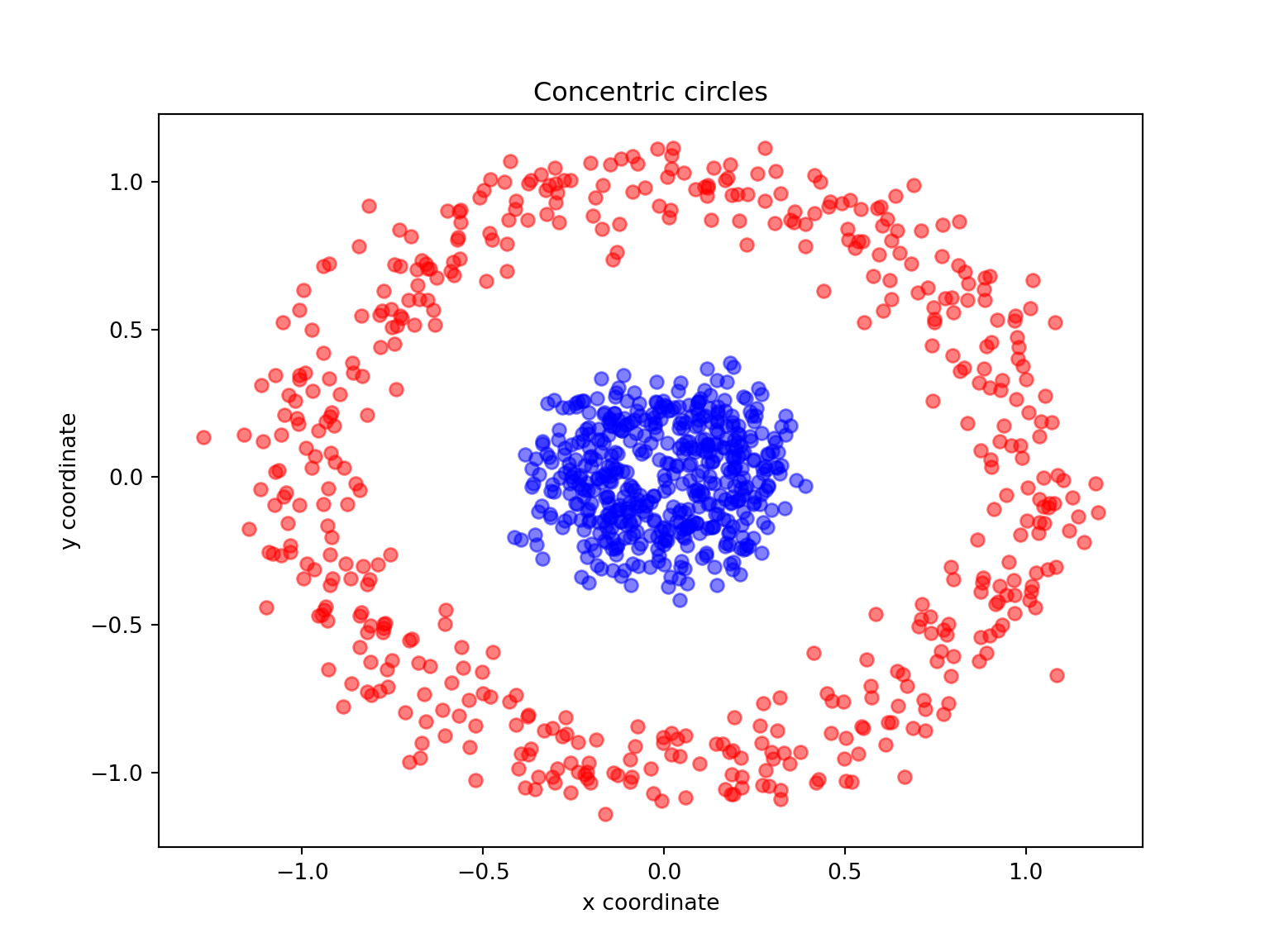

Again, perform both a linear and kernel PCA on the make_circles dataset

from sklearn.datasets import make_circles
from sklearn.decomposition import PCA, KernelPCA
import matplotlib.pyplot as plt
import numpy as np

X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)

#linear PCA 
scikit_pca = PCA(n_components=1)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X[y==0, 0], np.zeros((500,1))+0.1, color='red', alpha=0.5)
plt.scatter(X[y==1, 0], np.zeros((500,1))-0.1, color='blue', alpha=0.5)
plt.ylim([-15,15])

## (-15.0, 15.0)

plt.title('First principal component after Linear PCA')
plt.xlabel('PC1')
plt.show()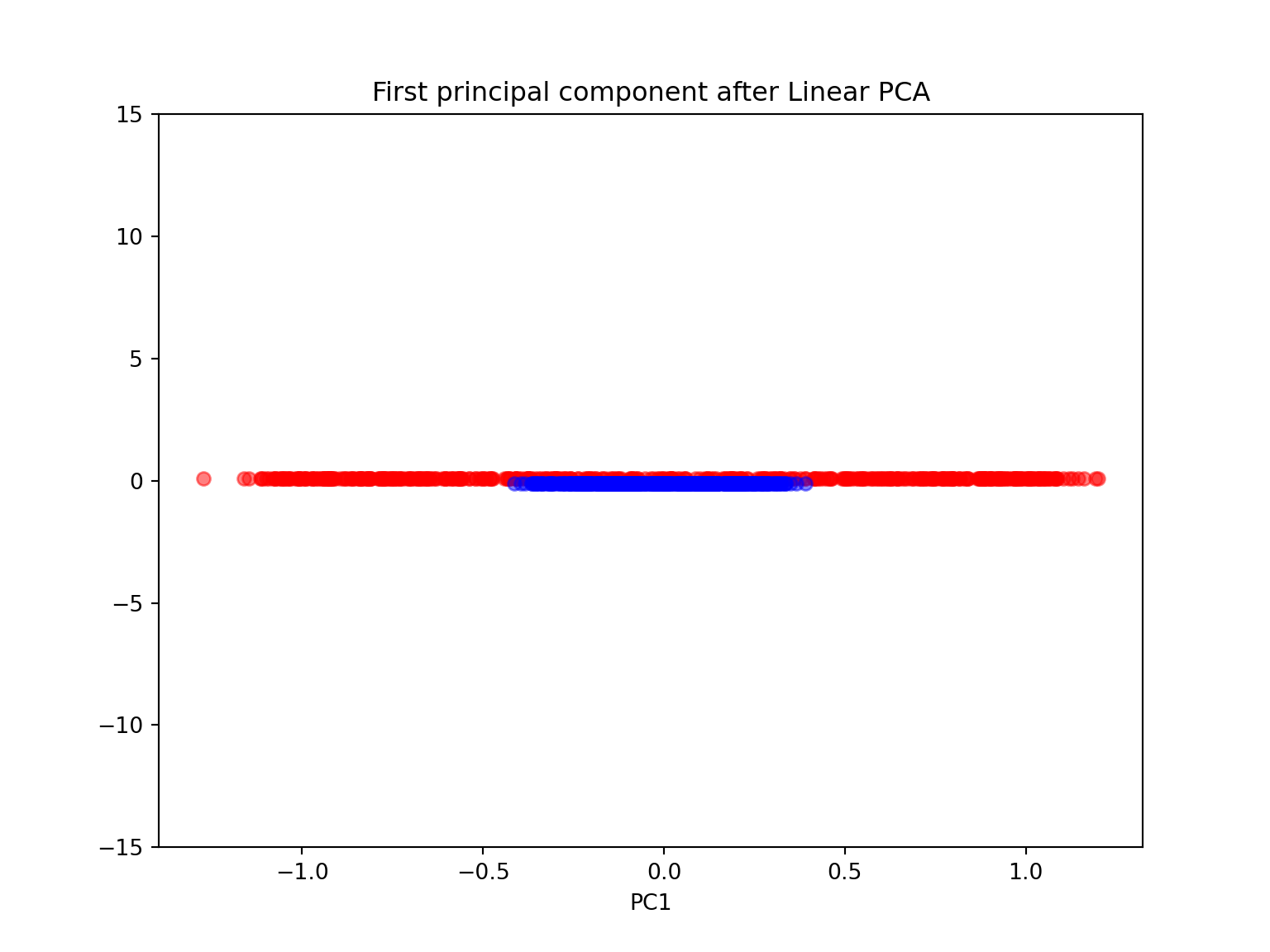

scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', alpha=0.5)
plt.ylim([-15,15])

## (-15.0, 15.0)

plt.title('First 2 principal component after Linear PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

#kernel PCA with n_components=1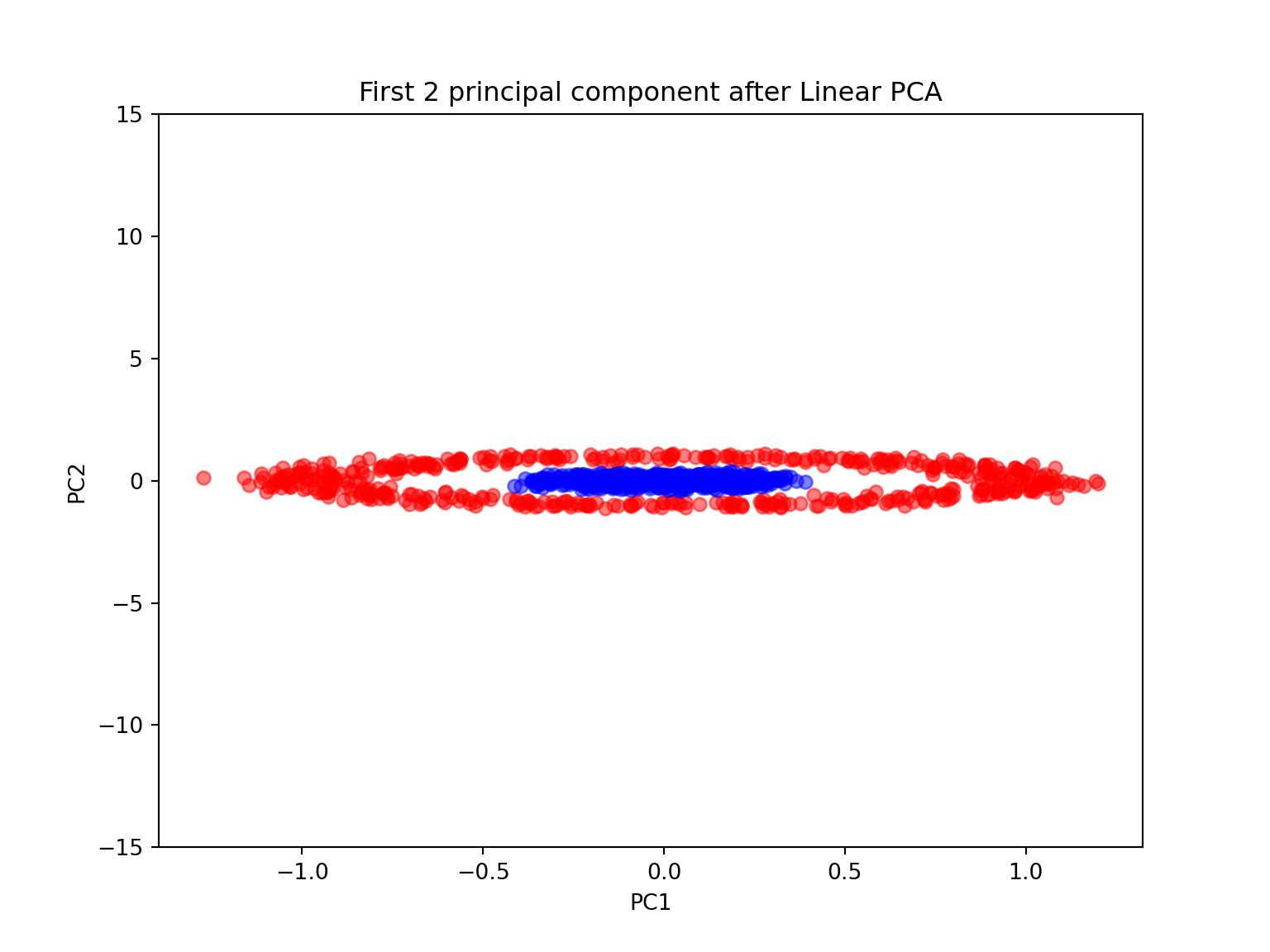

gamma = 15
X_pc = KernelPCA(gamma=15, n_components=1, kernel='rbf').fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_pc[y==0, 0], np.zeros((500,1)), color='red', alpha=0.5)
plt.scatter(X_pc[y==1, 0], np.zeros((500,1)), color='blue', alpha=0.5)

plt.title('First principal components after RBF Kernel PCA with $\gamma$={}'.format(gamma))
plt.xlabel('PC1')
plt.show()

#kernel PCA with n-components=2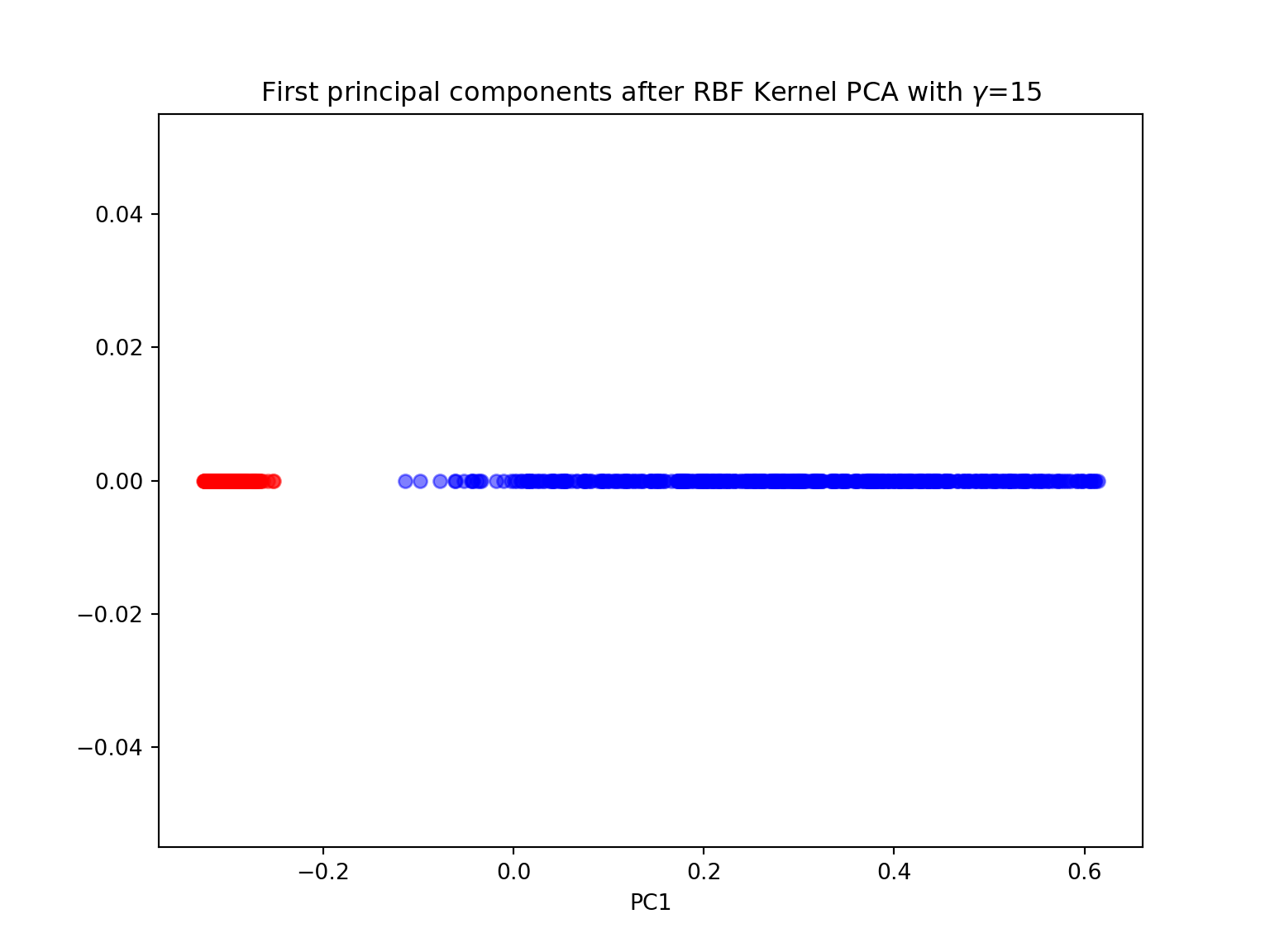

gamma = 15
X_pc = KernelPCA(gamma=gamma, n_components=2, kernel='rbf').fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_pc[y==0, 0], X_pc[y==0, 1], color='red', alpha=0.5)
plt.scatter(X_pc[y==1, 0], X_pc[y==1, 1], color='blue', alpha=0.5)

plt.title('First 2 principal components after RBF Kernel PCA with $\gamma$={}'.format(gamma))
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()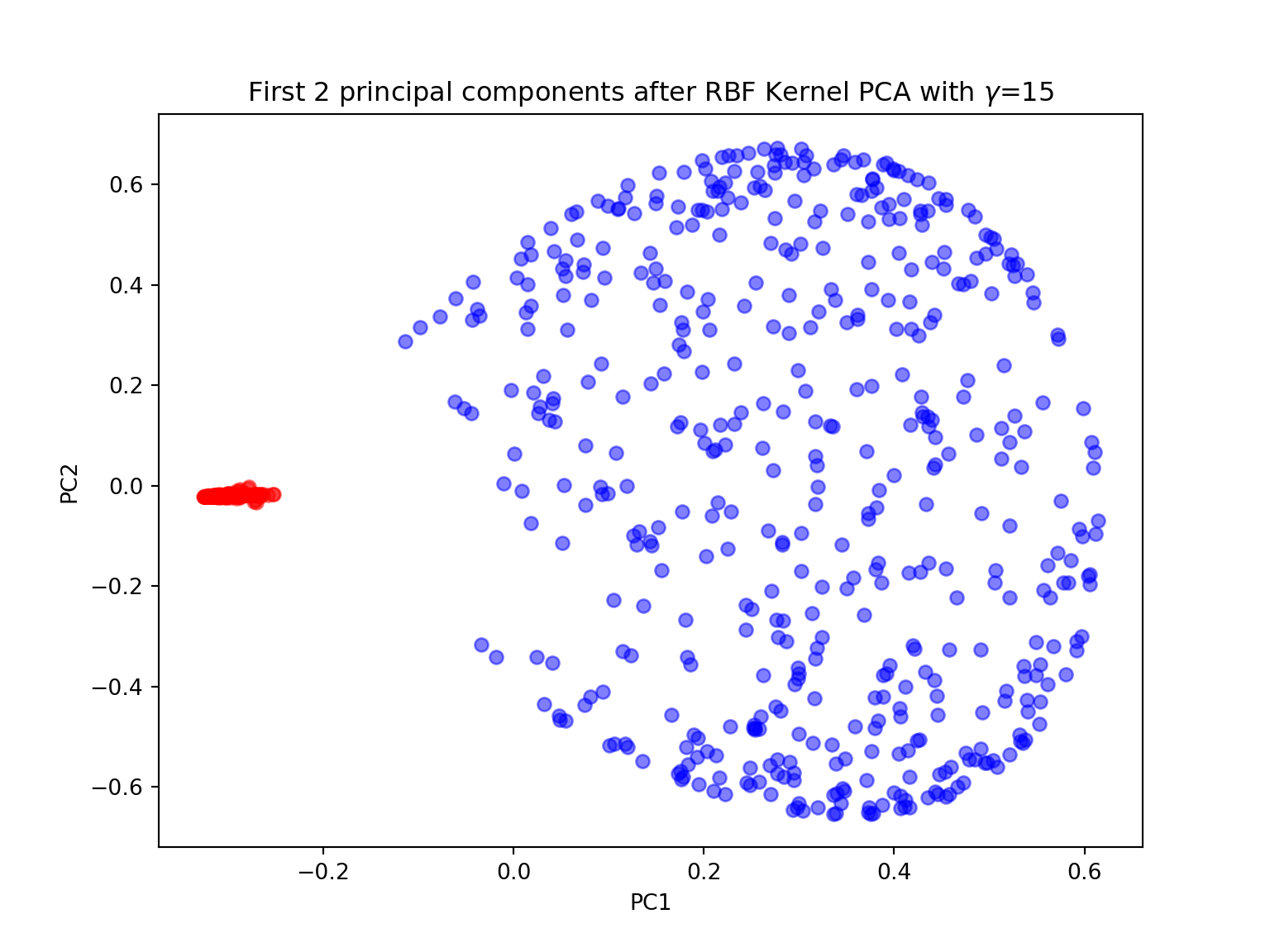

Swiss roll

Unrolling the Swiss roll is a much more challenging task (see Swiss roll).

from sklearn.datasets import make_swiss_roll
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

X, color = make_swiss_roll(n_samples=800, random_state=123)

fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.rainbow)
plt.title('Swiss Roll in 3D')
plt.show()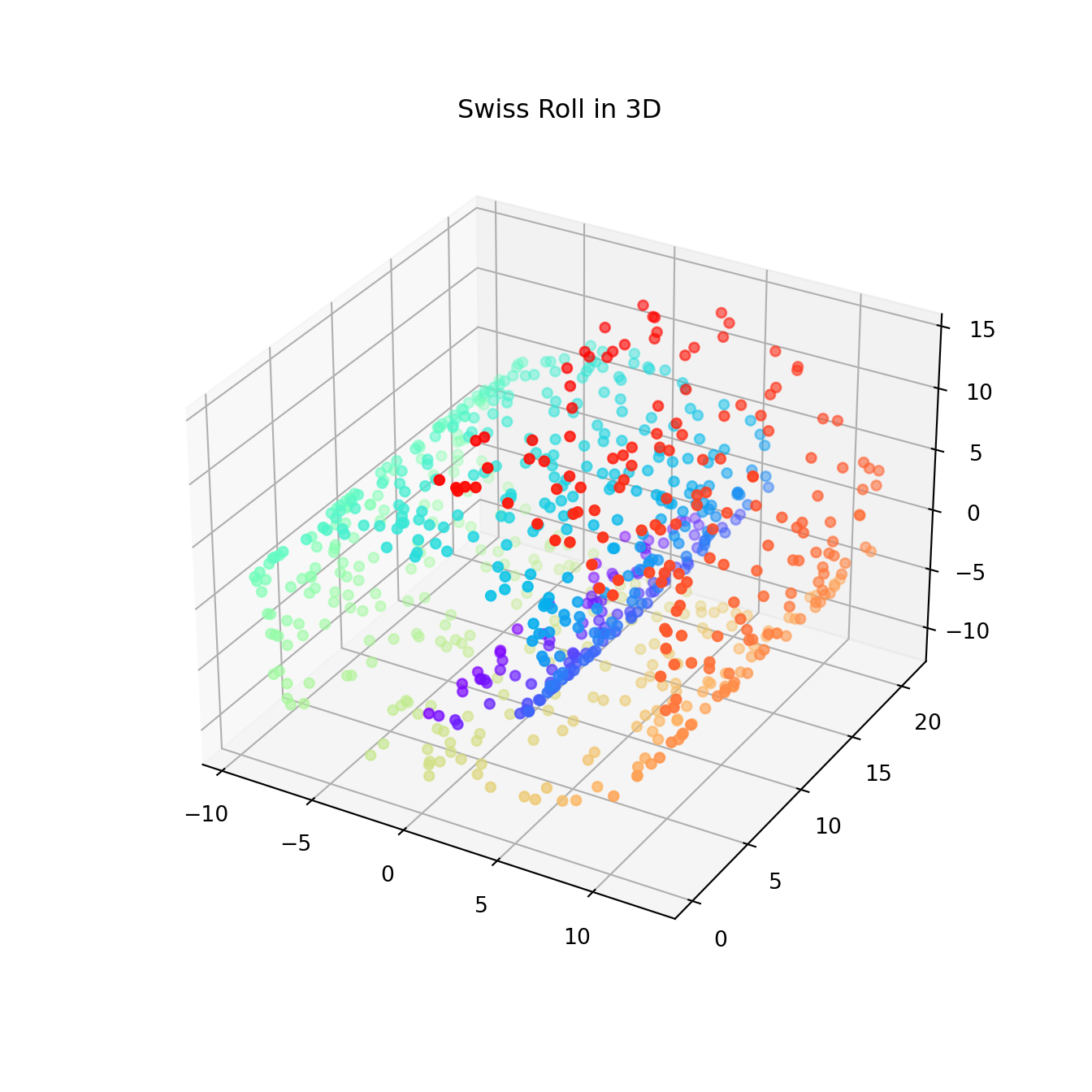

Again, try to perform both linear and kernel PCA on the Swiss roll dataset. Try with different values of \(\gamma\). Are you satisfied with the results?

from sklearn.datasets import make_swiss_roll
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from sklearn.decomposition import KernelPCA

gamma = 0.05
X, color = make_swiss_roll(n_samples=800, random_state=123)
X_pc = KernelPCA(gamma=gamma, n_components=2, kernel='rbf').fit_transform(X)

plt.figure(figsize=(8,6))
plt.scatter(X_pc[:, 0], X_pc[:, 1], c=color, cmap=plt.cm.rainbow)

plt.title('First 2 principal components after RBF Kernel PCA with $\gamma$={}'.format(gamma))
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()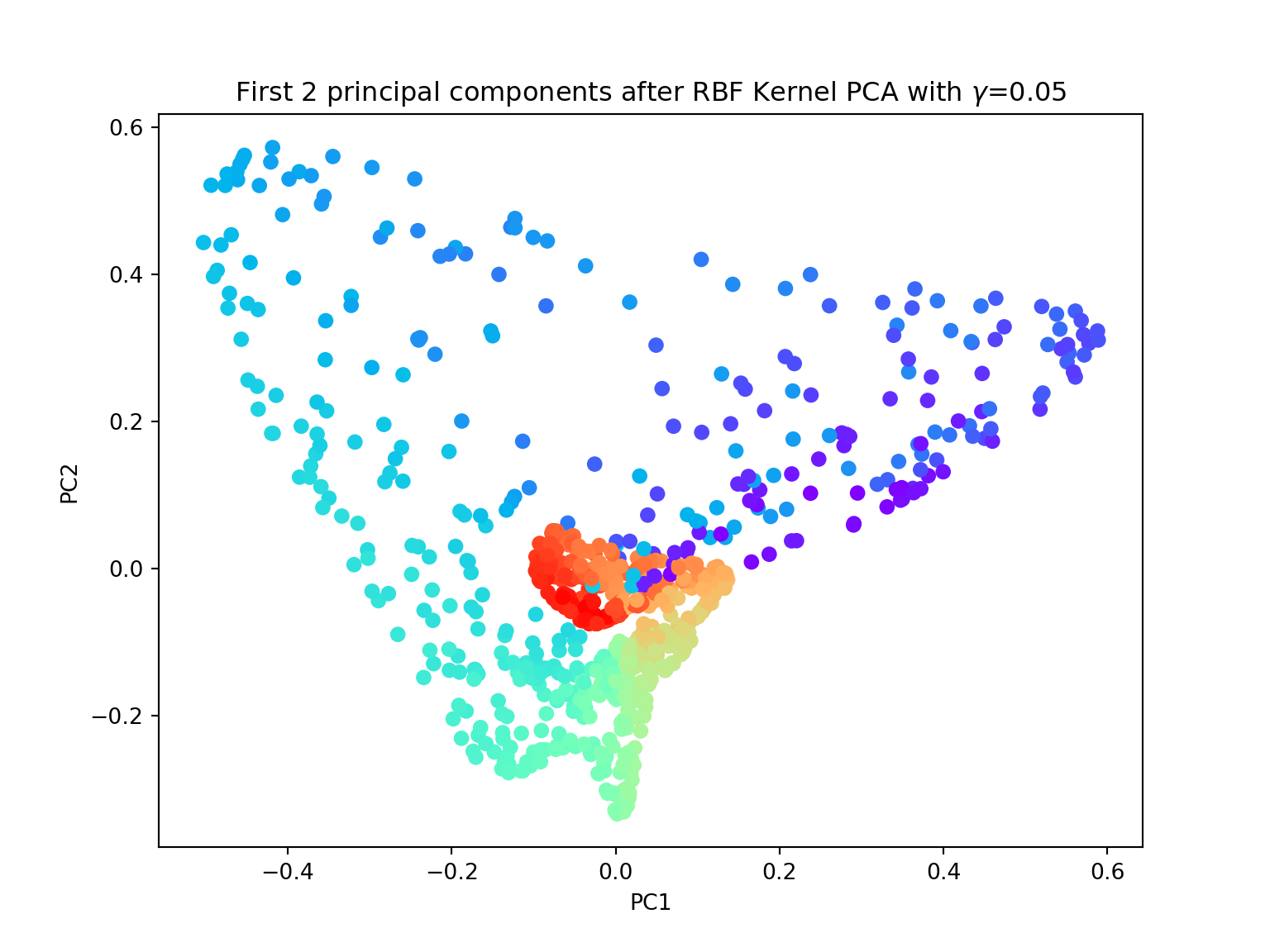

Locally Linear Embedding

In 2000, Sam T. Roweis and Lawrence K. Saul Nonlinear dimensionality reduction by locally linear embedding introduced an unsupervised learning algorithm called locally linear embedding (LLE) that is better suited to identify patterns in the high-dimensional feature space and solves our problem of nonlinear dimensionality reduction for the Swiss roll.

Locally linear embedding (LLE) seeks a lower-dimensional projection of the data which preserves distances within local neighborhoods. It can be thought of as a series of local Principal Component Analyses which are globally compared to find the best non-linear embedding.

Using the locally_linear_embedding class, ‘unroll’ the Swiss roll both in \(1\) and \(2\) dimensions.

import numpy as np
from sklearn.datasets import make_swiss_roll
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from sklearn.manifold import locally_linear_embedding

X, color = make_swiss_roll(n_samples=800, random_state=123)

# lle with n_components = 1

X_lle, err = locally_linear_embedding(X, n_neighbors=12, n_components=1)

plt.figure(figsize=(8,6))
plt.scatter(X_lle, np.zeros((800,1)), c=color, cmap=plt.cm.rainbow)

plt.title('First principal component after Locally Linear Embedding')
plt.show()

# lle with n_components = 2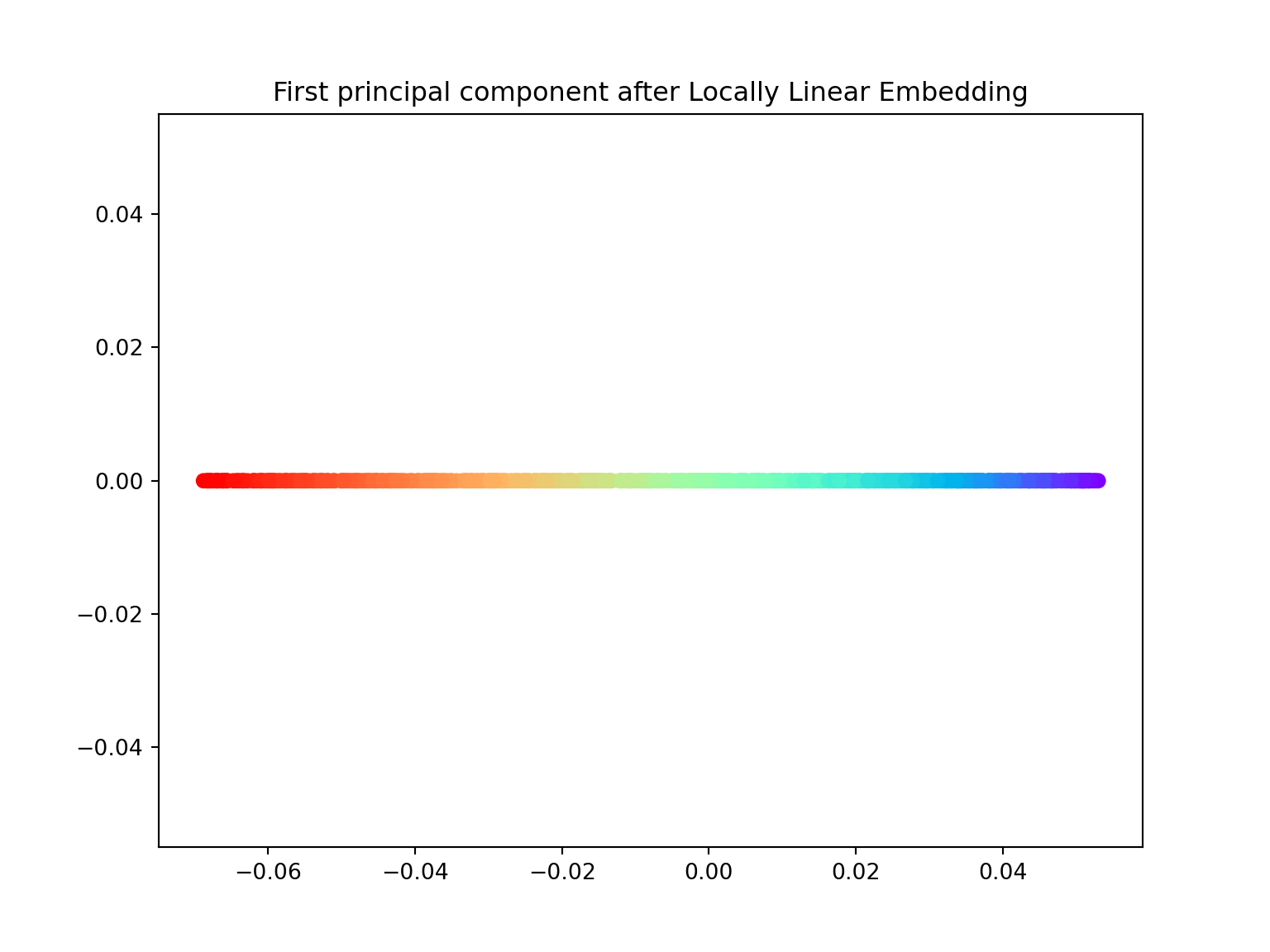

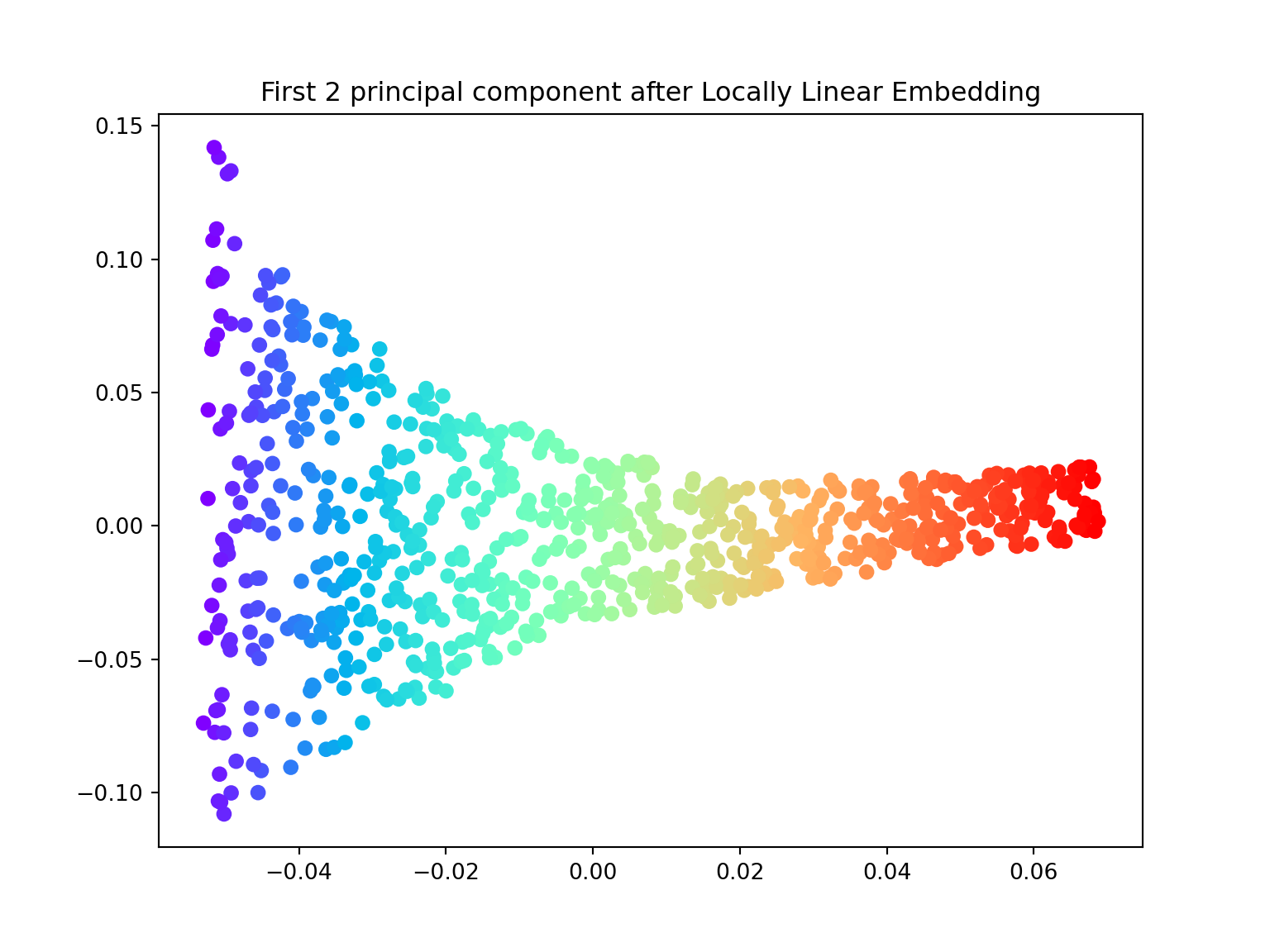
X_lle, err = locally_linear_embedding(X, n_neighbors=12, n_components=2)

plt.figure(figsize=(8,6))
plt.scatter(X_lle[:,0], X_lle[:,1], c=color, cmap=plt.cm.rainbow)

plt.title('First 2 principal component after Locally Linear Embedding')
plt.show()

Tutorial: nonlinear dimensionality reduction methods

MAP573 team

10/20/2020