library(mixtools)

Gaussian Mixture Models

We consider a collection of random variables \((X_1, \dots, X_n)\) associated with \(n\) individuals drawn from \(Q\) populations. The label of each individual describes the population (or class) to which it belongs and is unobserved. The \(Q\) classes have a priori distribution \({\boldsymbol \alpha} = (\alpha_1,\dots,\alpha_Q)\) with \(\alpha_q = \mathbb{P}(Z_i = q)\). In other word, the latent variable \(Z_i \in \{1,..,Q\}\) indicating the label follow a multinomial distribution \(Z_i \sim \mathcal{M}(1,\boldsymbol\alpha)\), such as \(\sum_{q=1}^Q \alpha_q = 1\).

The distribution of \(X_i\) conditional on the label of \(i\) is assumed to be a univariate gaussian distribution with unknown parameters, that is, \(X_i | Z_i = q \sim \mathcal{N}(\mu_q,\sigma^2_q)\).

We further introduce the additional notation \(Z_{iq} = \mathbb 1_{\{Z_i = q\}}\) and \(\tau_{iq}= \mathbb{P}(Z_{iq}=1|X_i)\) for posterior probabilities.

We denote the vector of parameters to be estimated by \(\mathbf{\mu} = (\mu_1,\dots,\mu_Q)\), \(\mathbf{\sigma^2} = (\sigma^2_1,\dots,\sigma^2_Q)\), \(\boldsymbol\tau = (\tau_{iq, i=1,\dots,n; q=1,\dots Q})\).

Questions

  1. Likelihood. Write the model complete-data loglikelihood.

  2. E-step. For fixed values of \(\hat{\mu}_q, \hat{\sigma}_{q}^{2}\) and \(\hat\alpha_q\), give the expression of the estimates of the posterior probabilities \(\tau_{iq}= \mathbb{P}(Z_{iq}=1|X_i)\).

  3. M-step. For fixed values of \(\hat{\tau}_{iq}\), show that the maximization step leads to the following estimator for the model parameters: \[ \hat{\alpha}_q = \frac 1n \sum_{i=1}^n \hat{\tau}_{iq}, \:\:\:\:\: \hat{\mu}_q = \frac{\sum_i \hat{\tau}_{iq} x_i}{\sum_i \hat{\tau}_{iq}}, \:\:\:\:\: \hat{\sigma}_q^2 = \frac{\sum_i \hat{\tau}_{iq} (x_i - \hat{\mu}_q)^2}{\sum_i \hat{\tau}_{iq}}. \]

  4. Implementation. Complete the following code.

get_cloglik <- function(X, Z, theta) {
  #returns the complete model loglikelihood
  n <- length(X); Q <- ncol(Z)
  alpha <- theta$alpha; mu <- theta$mu; sigma <- theta$sigma
  Xs <- # to write
  res <- # to write
  res
}

M_step <- function(X, tau) {
  #maximization step
  n <- length(X); Q <- ncol(tau)
  alpha  <- # to write
  mu     <- # to write
  sigma  <- # to write
  list(alpha = alpha, mu = mu, sigma = sigma)
}

E_step <- function(X, theta) {
  #expectation step
  probs <- # to write
  likelihoods <- rowSums(probs)
  list(tau = probs / likelihoods, loglik = sum(log(likelihoods)))
}
EM_mixture <- function(X, Q,
                       init.cl = base::sample(1:Q, n, rep=TRUE), max.iter=100, eps=1e-5) {
    n <- length(X); tau <- matrix(0, n, Q); tau[cbind(1:n, init.cl)] <- 1
    loglik  <- vector("numeric", max.iter)
    Eloglik <- vector("numeric", max.iter)
    iter <- 0; cond <- FALSE

    while (!cond) {
        iter <- iter + 1
        ## M step
        theta <- # to write
        ## E step
        res_Estep <- # to write
        tau <- # to write
        ## check consistency
        loglik[iter]  <- # to write
        Eloglik[iter] <- # to write
        if (iter > 1)
            cond <- (iter>=max.iter) | Eloglik[iter]-Eloglik[iter-1] < eps
    }

    res <- list(alpha = theta$alpha,  mu = theta$mu,  sigma = theta$sigma,
                tau   = tau, cl = apply(tau, 1, which.max),
                Eloglik = Eloglik[1:iter],
                loglik  = loglik[1:iter])
    res
}
  1. Examples. We would like now to assess the performance of our EM algorithm. To do so, we generate:
mu1 <- 5   ; sigma1 <- 1; n1 <- 100
mu2 <- 10  ; sigma2 <- 1; n2 <- 200
mu3 <- 15  ; sigma3 <- 2; n3 <- 50
mu4 <- 20  ; sigma4 <- 3; n4 <- 100
cl <- rep(1:4,c(n1,n2,n3,n4))
x <- c(rnorm(n1,mu1,sigma1),rnorm(n2,mu2,sigma2),
       rnorm(n3,mu3,sigma3),rnorm(n4,mu4,sigma4))
n <- length(x)

## we randomize the class ordering
rnd <- base::sample(1:n)
cl <- cl[rnd]
x  <- x[rnd]

alpha <- c(n1,n2,n3,n4)/n

curve(alpha[1]*dnorm(x,mu1,sigma1) +
      alpha[2]*dnorm(x,mu2,sigma2) +
      alpha[3]*dnorm(x,mu3,sigma3) +
      alpha[4]*dnorm(x,mu4,sigma3), 
      col="blue", lty=1, from=0,to=30, n=1000,
      main="Theoretical Gaussian mixture and its components",
      xlab="x", ylab="density")
curve(alpha[1]*dnorm(x,mu1,sigma1), col="red", add=TRUE, lty=2)
curve(alpha[2]*dnorm(x,mu2,sigma2), col="red", add=TRUE, lty=2)
curve(alpha[3]*dnorm(x,mu3,sigma3), col="red", add=TRUE, lty=2)
curve(alpha[4]*dnorm(x,mu4,sigma4), col="red", add=TRUE, lty=2)
rug(x)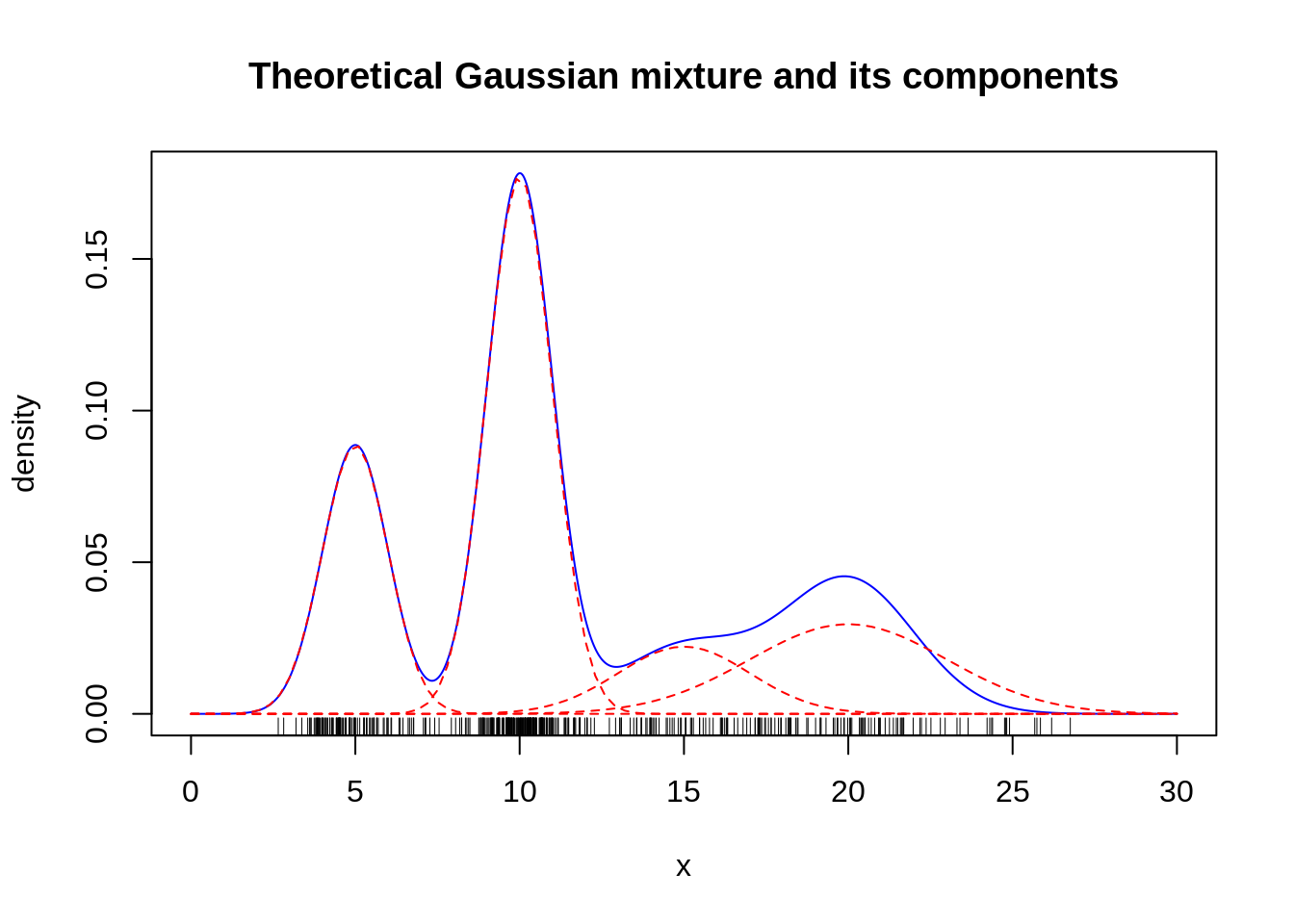

Try your EM algorithm on the simulated data. Comment the results. Consider different initialization. Compare with the output of the function normalmixEm in the package mixtools.

  1. Model Selection. Discuss the choice of \(Q\) by computing the BIC and ICL criterion and test it on your simulated data. \[ \mathrm{BIC}(Q) = - 2 \log L(X;\hat \alpha, \hat \mu, \hat \sigma^2) +\log(n) \mathrm{df}(Q). \] \[ \mathrm{ICL}(Q) = - 2 \log L(X,Z;\hat \alpha, \hat \mu, \hat \sigma^2) +\log(n) \mathrm{df}(Q). \]